KL-träskivor lämpar sig väl för stabilisering av byggnader då de har hög styvhet och bärförmåga. I en byggnad överförs normalt laster från bjälklag till stabiliserande väggar. En hel vägg består ofta av flera väggskivor som är sammankopplade med vertikala skarvar. Väggskivorna utsätts för en horisontell last i väggskivornas plan som ger skjuvspänningar och böjspänningar. Spänningarna i materialet ger tillsammans med förskjutningar i skarvarna en total deformation i skivans plan på grund av den horisontella lasten. I normala fall är deformationerna i skarvar och förband dimensionerande.
Om hela skivans skjuvmodul, Gmean och elasticitetsmodul, Emean är känd kan den totala deformationen, δtot skrivas som:
6.6 \({\delta _{{\rm{tot}}}} = {\delta _{{\rm{skjuv}}}} + {\delta _{{\rm{böj}}}} + {\delta _{\rm skarv}}\)
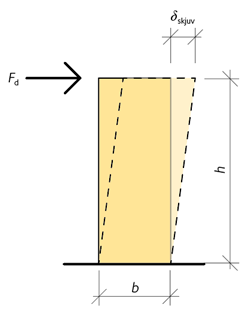
Deformation på grund av tvärkrafter, se figur 6.4, kan uttryckas enligt ekvation 6.7:
6.7 \({\delta _{{\rm{skjuv}}}} = \frac{{{F_{\rm{d}}} \cdot h}}{{b \cdot {t_{\rm tot}} \cdot {G_\rm {mean}}}}\)
där:
| Fd | är dimensionerande horisontell last som verkar på skivan. |
| h | är skivans höjd. |
| b | är skivans bredd. |
| Gmean | är skivans skjuvmodul. |
| ttot | är skivans totala tjocklek. |
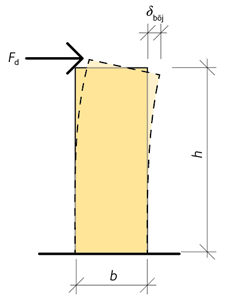
Skivans deformation på grund av moment, se figur 6.5, kan uttryckas enligt ekvation 6.8:
6.8 \({\delta _{{\rm{böj}}}} = \frac{{{F_{\rm{d}}} \cdot {h^3}}}{{3 \cdot {E_\rm {mean}} \cdot I}}\)
där:
| Fd | är dimensionerande horisontell last som verkar på skivan. |
| h | är skivans höjd. |
| Emean | är skivans elasticitetsmodul. |
| I | är skivans tröghetsmoment. |
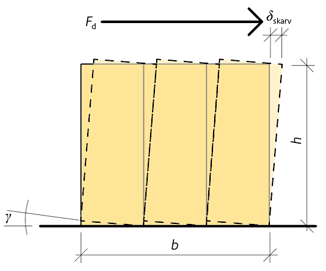
Skivornas deformation på grund av förskjutningar i skarvar, se figur 6.6, kan uttryckas enligt ekvation 6.9:
6.9 \({\delta _{{\rm{fog}}}} = \gamma \cdot h = \Delta \gamma \frac{h}{b}\)
där:
| h | är skivans höjd. |
| b | är skivans bredd. |
| γ | är vinkeländring i radianer. |
6.10 \(\Delta \gamma = \frac{{{F_{\rm{d}}}}}{{{K_{{\rm{ser}}}}}}\)
där:
| Fd | är dimensionerande horisontell last som verkar på skivorna. |
| Kser | är skarvens styvhet. |
Skarvens styvhetsvärden och även skivans styvhet bestäms av förbandets utformning och skivornas uppbyggnad. Tillverkare och leverantörer av skruvar och beslag kan i många fall bidra med underlag till styvhetsvärden. I tabell 6.3 och tabell 6.4 anges ungefärliga värden för några olika förband och skivor.
För kontroll av skjuvspänningar se avsnitt 3.3.5.
Figur 6.4 KL-träskivans deformation på grund av tvärkrafter.
Figur 6.5 KL-träskivans deformation på grund av moment.
Figur 6.6 KL-träskivornas deformation på grund av förskjutningar i skarvar.
Tabell 6.3 Karakteristiska värden per skruvpar i brottgränstillstånd och bruksgränstillstånd för ett förband som består av träskruv Spax 5 × 40, eller likvärdiga, och plywoodremsa 12 × 60 i hållfasthet P30, eller likvärdig. Centrumavståndet mellan träskruvarna ska vara större än 40 mm. Dessa värden är empiriskt framtagna.
| Brottgränstillstånd FRk (kN/skruvpar) |
Bruksgränstillstånd Kser (kN/mm och skruvpar) |
| 1,5 1) | 0,5 2) |
1) Maxlast vid 9 mm deformation.
2) Styvhetsvärdet gäller för deformationer upp till 2 mm.
Tabell 6.4 Egenskaper hos KL-träskivor för beräkning i bruksgränstillståndet vid belastning i väggskivans plan. Styvhetsvärdena är baserade på hela tvärsnittet, bruttoyta.
| Skivtjocklek (mm) |
Skjuvmodul Gmean (N/mm2) |
Elasticitetsmodul Em,0,mean (N/mm2) |
| 80 (3-skikt) | 400 | 6 400 |
| 100 (3-skikt) | 400 | 5 700 |
| 120 (5-skikt) | 400 | 6 200 |

