Med minskande spännvidd/höjdförhållande gäller inte längre linjär spänningsfördelning enligt balkteorin. För väggbalkar med ungefär \(l\) / h ≤ 4 blir icke-linjärt beteende märkbart och det måste beaktas vid \(l\) / h ≤ 2. Kantspänningar vid beräkning enligt platteori beror på lasten vid skivans övre och nedre del och på \(l\) / h-förhållandet.
Vid kontinuerliga system påverkar skjuvdeformationen de inre krafterna. Moment vid upplag minskar och moment i fältmitt ökar. Därför rekommenderas att moment och böjspänningar samt böjdeformationer bestäms utifrån en fritt upplagd balk i det längsta spannet. Upplagskrafter och tvärkrafter kan bestämmas utifrån en kontinuerlig balk.
Förutsättningar:
En vertikalt och horisontellt belastad väggskiva, med två spann med längderna \(l\)1 = 4,5 m och \(l\)2 = 6,5 m och höjden h = 3 m, se figur 6.23.
Laster:
- Egentyngd från tak ovanför väggen är gk = 4,0 kN/m och från vägg och bjälklag i nederkant är gk = 7,7 kN/m.
- Nyttig last som belastar i nederkant är nk = 6,0 kN/m.
- Snölast som belastar i ovankant är sk = 3,5 kN/m.
- Laster och lastfaktorer enligt tabell 6.10.
Väggen består av en 5-skiktsskiva av KL-trä, med tjockleken 30+20+30+20+30 = 130 mm och med samtliga skikt av brädor i hållfasthetsklass C24. Klimatklass 1, säkerhetsklass 3 (γd = 1).
För KL-trä med enbart brädor i hållfasthetsklass C24 gäller enligt tabell 3.7:
E0,x,0,05 = 7 400 MPa
E0,x,mean = 11 000 MPa
G9090,xlay,mean = 50 MPa
G090,xlay,mean = 690 MPa
Enligt tabell 3.6 gäller:
fm,k = 24 MPa
fc,0,k = 21 MPa
fv,k = 4 MPa
Med γM = 1,25 enligt tabell 3.2 och kmod = 0,8 enligt tabell 3.3 (nyttig last huvudlast = medellång) blir dimensionerande hållfastheter:
\({f_{{\rm{m}},{\rm{d}}}} = \frac{{{k_{{\rm{mod}}}} \cdot {f_{{\rm{m}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}} = \frac{{0,8 \cdot 24}}{{1,25}} = 15,36\;{\rm{MPa}}\)
\({f_{{\rm{c}},0,{\rm{d}}}} = \frac{{{k_{{\rm{mod}}}} \cdot {f_{{\rm{c}},0,{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}} = \frac{{0,8 \cdot 21}}{{1,25}} = 13,44\;{\rm{MPa}}\)
\({f_{{\rm{v}},{\rm{d}}}} = \frac{{{k_{{\rm{mod}}}} \cdot {f_{{\rm{v}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}} = \frac{{0,8 \cdot 4}}{{1,25}} = 2,56\;{\rm{MPa}}\)
Beräkningar:
Dimensionerande lastkombination för vertikal last:
\(\begin{array}{l} {q_{\rm{d}}} = {\gamma _{\rm{G}}} \cdot {g_{\rm{k}}} + {\gamma _{{\rm{Q,n}}}} \cdot {n_{\rm{k}}} + {\gamma _{{\rm{Q,s}}}} \cdot {\Psi _{0,{\rm{s}}}} \cdot {s_{\rm{k}}} = \\ = 0,89 \cdot 1,35 \cdot 11,7 + 1,5 \cdot 6,00 + 1,5 \cdot 0,8 \cdot 3,5 = 27,3\;{\rm{kN/m}} \end{array}\)
Moment
Dimensionerande moment för en enkelspänd balk med längden \(l\)2 = 6,5 m:
\({M_{\rm{d}}} = \frac{{{q_{\rm{d}}} \cdot {l_2}^2}}{8} = \frac{{27,3 \cdot {{6,5}^2}}}{8} = 144,2{\rm{\;kNm}}\)
Tvärsnittet vid böjning beräknas för de horisontella skikten, det vill säga enbart brädskikten i bärriktningen:
\({W_{{\rm{z}},{\rm{net\;}}}} = \;\frac{{{d_\rm z} \cdot {h^2}}}{6} = \frac{{0,04 \cdot {3^2}}}{6} = 0,06\;{{\rm{m}}^3}\)
med dz = totala brädtjockleken för de horisontella skikten:
\({\sigma _{\rm{d}}} = \frac{{{M_{\rm{d}}}}}{{{W_{{\rm{z}},{\rm{net}}}}}} = \frac{{144,2 \cdot {{10}^3}}}{{0,06 \cdot {{10}^6}}} = 2,40{\rm{\;MPa}}<{f_{\rm m,d}} = 15,36\;{\rm{MPa}}\)
Tvärkraft
Dimensionerande tvärkraft:
\({V_{\rm{d}}} = 0,625 \cdot {q_{\rm{d}}} \cdot {l_2} = 0,625 \cdot 27,3 \cdot 6,5 = 110,9\;{\rm{kN}}\)
\({A_{{\rm{z}},{\rm{net\;}}}} = {d_{\mathop{\rm z}\nolimits} } \cdot h = 0,04 \cdot 3 = 0,12\;{{\rm{m}}^2}\)
med dz = totala brädtjockleken för de horisontella skikten:
\({\tau _{\rm{d}}} = 1,5 \cdot \frac{{{V_{\mathop{\rm d}\nolimits} }}}{{{A_{{\rm{z}},{\rm{net}}}}}} = 1,5 \cdot \frac{{110,9 \cdot {{10}^3}}}{{0,12 \cdot {{10}^6}}} = 1,38{\rm{\;MPa}}<{f_{{\mathop{\rm v}\nolimits} ,\rm d}} = 2,56\;{\rm{MPa}}\)
Tryckkraft
Lastspridning från upplag beräknas med vinkeln 30° ut från stödet upp till höjden h / 4.
Upplagsreaktion:
\({M_\rm B} = - \frac{{{q_\rm d}{l_1}^3 + {q_\rm d}{l_2}^3}}{{8\left( {{l_1} + {l_2}} \right)}} = \frac{{27,3 \cdot {{4,5}^3} + 27,3 \cdot {{6,5}^3}}}{{8\left( {4,5 + 6,5} \right)}} = 113\;{\rm{kNm}}\)
\({R_\rm B} = \frac{{{q_\rm d}{l_1}}}{2} + \frac{{{q_\rm d}{l_2}}}{2} - \frac{{{M_\rm B}}}{{{l_1}}} - \frac{{{M_\rm B}}}{{{l_2}}} = \frac{{27,3 \cdot 4,5}}{2} + \frac{{27,3 \cdot 6,5}}{2} - \frac{{113}}{{4,5}} - \frac{{113}}{{6,5}} = 193\;{\rm{kN}}\)
Lastspridning:
\({B_{{\rm{uppl}}}} = 2 \cdot \frac{h}{4} \cdot \tan \left( {30^\circ } \right) = 2 \cdot \frac{3}{4} \cdot 0,577 = 0,86\;{\rm{m}}\)
Det vill säga att upplagsreaktionen sprids på en bredd av 0,86 m med en kraft av:
\({n_\rm d} = \frac{{{R_\rm B}}}{{{B_\rm {uppl}}}} = \frac{{193}}{{0,86}} = 224\;{\rm{kN/m}}\)
Kontroll av knäckning görs för en strimla av 1,0 m vilket ger kraften:
\({n_{1,{\rm{d}}}} = \frac{{{n_{\rm{d}}}}}{{{B_{{\rm{uppl}}}}}} = \frac{{224}}{{0,86}} = 260\;{\rm{kN/m}}\)
Kontroll av knäckning
Egenskaperna för 5-skiktsskivan blir enligt tabell 6.11.
Knäckning kontrolleras i brottgränstillstånd:
\(\frac{{{\sigma _{{\rm{c}},0,{\rm{d}}}}}}{{{k_{{\rm{c}},{\rm{y}}}} \cdot \;{f_{{\rm{c}},0,{\rm{d}}}}}} \le 1\)
Reduktionsfaktorn kc,y kan skrivas som:
\({k_{{\rm{c}},{\rm{y}}}} = \frac{1}{{{k_{\rm{y}}} + \sqrt {k_{\rm{y}}^2 - \lambda _{{\rm{rel}},{\rm{y}}}^2} }} = \frac{1}{{1,395 + \sqrt {{{1,395}^2} - {{1,30}^2}} }} = 0,526\)
där:
\({k_{\rm{y}}} = 0,5\left( {1 + 0,1\left( {{\lambda _{{\rm{rel}},{\rm{y}}}} - 0,3} \right) + \lambda _{{\rm{rel}},{\rm{y}}}^2} \right) = \\ = 0,5\left( {1 + 0,1\left( {1,30 - 0,3} \right) + {{1,30}^2}} \right) = 1,395\)
där:
\({\lambda _{{\rm{rel}},{\rm{y}}}} = \frac{{{\lambda _{\rm{y}}}}}{\pi }\sqrt {\frac{{\;{f_{{\rm{c}},0,{\rm{k}}}}}}{{{E_{0,05}}}}} = \frac{{76,7}}{\pi }\sqrt {\frac{{21}}{{7400}}} = 1,30\)
\({\sigma _{{\rm{c}},0,{\rm{d}}}} = \frac{{{n_{1,d}}}}{{{A_{{\rm{x}},{\rm{net}}}}}} = \frac{{260 \cdot {{10}^3}}}{{900 \cdot {{10}^2}}} = 2,88{\rm{\;MPa}}\)
\(\frac{{{\sigma _{{\rm{c}},0,{\rm{d}}}}}}{{{k_{{\rm{c}},{\rm{y}}}} \cdot \;{f_{{\rm{c}},0,{\rm{d}}}}}} = \frac{{2,88}}{{0,526 \cdot 13,44}} = 0,41 \le 1\) OK
Väggen klarar tryckbelastningen, utnyttjandegraden är 41 procent.
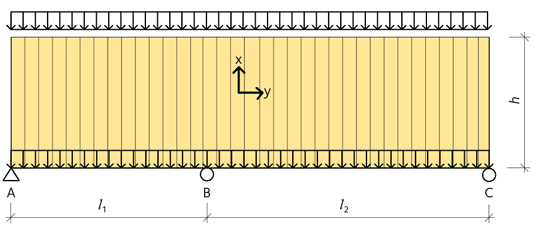
Figur 6.23 Väggskiva på pelarstöd.
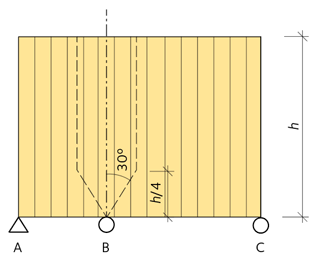
Figur 6.24 Lastspridning av stödreaktion.
Tabell 6.10 Laster och lastfaktorer.
| Last | kN/m2 | γg, γQ | Lastvaraktighetsklass | kmod | Ψ0 | Ψ1 | Ψ2 |
| gk | 11,7 | 0,89 ⋅ 1,35 | Permanent (P) | 0,6 | – | – | – |
| nk | 6,00 | 1,5 | Medellång (M) | 0,8 | 0,7 | 0,5 | 0,3 |
| sk | 3,50 | 1,5 | Medellång (M) | 0,8 | 0,8 | 0,6 | 0,2 |
Tabell 6.11 Egenskaper för 5-skikts symmetrisk skiva av KL-trä, strimla med bredd bx = 1,05 m. Skivtjocklek 130 mm (30/20/30/20/30).
| Egenskap | Beräkningsformel |
| Tvärsnittsarean (mm2) |
\({A_\rm {x,net}} = {b_\rm x} \cdot 3 \cdot {t_1}\) |
| Gammavärden | \({\gamma _3} = 1\quad {\gamma _1} = {\gamma _5} = \frac{1}{{1 + \frac{{{\pi ^2}{E_{{\rm{x}},5}}{t_5}}}{{l_{{\rm{ref}}}^2}} \cdot \;\frac{{{t_4}}}{{{G_{9090,4}}}}}}\) |
| Effektivt böjmotstånd (mm4) |
\(\begin{array}{c} {I_{{\rm{x}},{\rm{ef}}}} = \frac{{{b_x}t_1^3}}{{12}} + {\gamma _1}{b_x}{t_1}{a_1}^2 + \frac{{{b_x}t_3^3}}{{12}} + \frac{{{b_x}t_5^3}}{{12}} + {\gamma _5}{b_x}{t_5}{a_5}^2 = \\ = {b_x} \cdot \left( {\frac{{3 \cdot t_1^3}}{{12}} + 2{\gamma _1}{t_1}{a_1}^2} \right) \end{array}\) |
| Tröghetsradie ix,ef |
\({i_{{\rm{x}},{\rm{ef}}}} = \sqrt {\frac{{{I_{{\rm{x}},{\rm{ef}}}}}}{{{A_{{\rm{x}},{\rm{net}}}}}}} \) |
| Slankhetsfaktor λy |
\({\lambda _{\mathop{\rm y}\nolimits} } = \frac{{{l_\rm k}}}{{{i_{{\mathop{\rm x}\nolimits} \rm ,ef}}}}\) |
| Egenskap | Applikation till exempel |
| Tvärsnittsarean (mm2) |
\({A_\rm {x,net}} = 1000 \cdot 3 \cdot 30 = 900 \cdot {10^2}\;{\rm{m}}{{\rm{m}}^2}\) |
| Gammavärden | \({\gamma _3} = 1\quad {\gamma _1} = {\gamma _5} = \frac{1}{{1 + \frac{{{\pi ^2}11000 \cdot 30}}{{{{3000}^2}}} \cdot \;\frac{{20}}{{50}}}} = 0,874\) |
| Effektivt böjmotstånd (mm4) |
\(\begin{array}{c} {I_{{\rm{x}},{\rm{ef}}}} = 1000 \cdot \left( {\frac{{3 \cdot {{30}^3}}}{{12}} + 2 \cdot 0,874 \cdot 30 \cdot {{50}^2}} \right) = \\ = 13785 \cdot {10^4}\;{\rm{m}}{{\rm{m}}^4} \end{array}\) |
| Tröghetsradie ix,ef |
\({i_{{\rm{x}},{\rm{ef}}}} = \sqrt {\frac{{13785 \cdot {{10}^4}}}{{900 \cdot {{10}^2}}}} = 39,1\;{\rm{mm}}\) |
| Slankhetsfaktor λy |
\({\lambda _{\mathop{\rm y}\nolimits} } = \frac{{3000}}{{39,1}} = 76,7\) |

