Bjälklag av konstruktionsvirke, ej lägenhetsskiljande

Träbjälklag i bostadshus

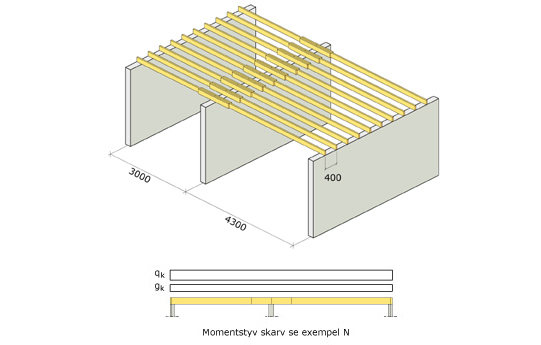
Bild 1 och bild 2.

Momentstyv skarv. Mått enligt figurer. Undergolv av spånskiva spiklimmas mot golvbjälkarna. Sådan limning får anses ge samverkan vid kontroll av sviktegenskaperna men inte i övrigt. Kontroll ska utföras enligt eurokoder.

1. Förutsättningar

Hållfasthetsklass: C24

Klimatklass: 1

Säkerhetsklass: 2  (γ_d = 0,91)

Lastvärden

Bjälklagets egentyngd: g_k =0,85 kN/m². Egentyngden klassificeras som permanent bunden last.
 
Nyttig last enligt lastkategori A, Bostäder o.dyl. – Bjälklag: q_k = 2,0 kN/m² och Q_k = 2,0 kN.  Nyttig last klassificeras som variabel, fri last.

Lasten per bjälke av
bjälklagets egentyngd: g_k = 0,4 · 0,85 = 0,34 kN/m
nyttig last: q_k = 0,4 · 2,0 = 0,8 kN/m

2. Preliminär dimensionering

Tabellerna för Hjälpmedel - tabeller avser bjälklag med centrumavstånd 600 mm och är ej tillämpliga. Pröva 45x220 mm.

3. Kontroll av brottgränstillståndet

Dimensionerande lastvärde i brottgränstillståndet kan tecknas enligt ekvation 6.10.b i SS-EN 1990

q_d = Σ γ_d 0,89·1,35 G_k + γ_d 1,5 Q_k (huvudlast) + Σ γ_d 1,5 ψ₀ Q_k (övriga laster)
q_d = 0,91· 0,89 · 1,35 · 0,34 + 0,91 · 1,5 · 0,8 = 1,46 kN/m

Lasteffekter böjning

Dimensionerande moment uppträder vid innerstöd när nyttig last uppträder i båda facken.

Eftersom bjälkarnas överkant hindras av golvskivan från att förskjutas i sidled föreligger ingen risk för vippning.

\(M_d = \frac{q_d \cdot {l_1}^3 + q_d \cdot{l_2}^3 }{8 \cdot \left(l_1 + l_2 \right)}\)

\(M_d = - \frac{1,46 \cdot 4,3^3 + 1,46 \cdot 3,0^3}{8 \cdot (4,3 + 3,0)} = -2,66 \: \text{kNm}\)

\(\sigma_{m,d} = \frac{2,66 \cdot 10^3 \cdot 6}{0,045 \cdot 0,220^2} = 7,33 \cdot 10^6 \: N/m^2 = 7,33 \: \text{MPa}\)

Bärförmåga böjning

Dimensionerande värde på böjhållfasthet blir med

k_mod = 0,80 (C24, lastvaraktighetsklass medellång, klimatklass 1)

f_m,k = 24 MPa (C24)

γ_m = 1,3

\(f_{m,d} = \frac{k_{mod} \cdot f_{m,k}}{\gamma_m} = \frac{0,8 \cdot 24}{1,3} = 14,7 \: \text{MPa} \)

\(f_{m,d} > \sigma_{m,d}\) OK!

Lasteffekter skjuvning

Dimensionerande tvärkraft uppträder även den vid innerstöd och för samma lastställning

\(V_d = \frac{q_d \cdot l_1}{2} - \frac{M_d}{l_1}\)

\(V_d = \frac{1,46 \cdot 4,3}{2} + \frac{2,66}{4,3} = 3,76 \: \text{kN}\)

\(\tau_d = \frac{1,5 \cdot 3,76
\cdot 10^3}{0,045 \cdot 0,220} =
0,57 \cdot 10^6 \: \text{N/m^2} =
0,57 \: \text{MPa}\)

Bärförmåga skjuvning

Dimensionerande värde på skjuvhållfasthet blir med

k_mod = 0,80 (C24, lastvaraktighetsklass medellång, klimatklass 1)

f_v,k = 4,0 MPa (C24)

γ_m = 1,3

Enligt allmänt råd i EKS 9, BFS 2013:10, bör kcr enligt nedan användas för virke som inte är exponerat för nederbörd och solstrålning.

\(k_{cr} = min \begin{cases} \frac{3,0}{f_{v,k}} \\ 1,0 \end{cases}\)

 alltså k_cr = 0,75

\(f_{v,d} = \frac {k_{cr} \cdot k_{mod} \cdot f_{v,k}} {\gamma_m} =
\frac{0,75 \cdot 0,80 \cdot 4,0}{1,3}= 1,85 \:\text{MPa}\)

\(f_{v,d} > \tau_d\) OK!

4. Kontroll av bruksgränstillståndet

Funktionskriterier

Deformationerna hos en konstruktion under påverkan av laster ska begränsas med hänsyn till risken för skador samt med hänsyn till funktionskrav och estetiska krav. Gränsvärden för nedböjningar bestäms från fall till fall, och gränsvärden med hänsyn till utseende eller komfort kan anges av byggherren. Gränsvärde för w_inst och w_fin väljs till L/300 =4300/300=14,33 mm.

Den omedelbara nedböjningen, w_inst, kan beräknas för den karakteristiska lastkombinationen med användande av medelvärde på elasticitetsmodul, skjuvmodul och förskjutningsmodul. Den slutliga nedböjningen, w_fin, kan förenklat beräknas som

w_fin = w_fin,G + w_fin,Q,1

där

w_fin,G = w_inst,G (1+k_def),
w_fin,Q,1 = w_inst,Q,1 (1+ψ_2,1∙k_def) för huvudlasten där ψ_2,1 är faktor för kvasipermanentvärdet av variabel last,
k_def = 0,60 för klimatklass 1.

Den största nedböjningen uppträder i 4,3-metersfacket när enbart detta fack belastas med nyttig last.

\(W_{max} = \frac{5}{384} \cdot
\frac{q \cdot {l_1}^4}{E_{0,mean}
\cdot I} - \frac{M_s \cdot l^2}
{16 \cdot E_{0,mean}\cdot I}\)

där
q = last i 4,3-metersfacket
M_s = stödmomentet
E_0,mean = medelvärde på elasticitetsmodulen = 11000 MPa (C24)

\(M_{sgk} = - \frac{g_k \cdot
{l_1}^3 + g_k \cdot {l_2}^3}{8
\cdot (l_1 + l_2)} = -
\frac{0,34 \cdot 4,3^3 + 0,32
\cdot 3.0^3}{8 \cdot (4,3 + 3,0)}
=0,620 \: \text{kNm}\)

\(M_{sqk} = - \frac{ q_k \cdot {l_1}^3 + q_k \cdot {l_2}^3}{8 \cdot (l_1
+ l_2)} = - \frac{0,34 \cdot 4,3^3 + 0,32 \cdot 3.0^3}{8 \cdot (4,3 +
3,0)} =0,620 \: \text{kNm} \)

Eftersom golvbjälkarna är skarvade med spikförband över innerstödet, beräknas nedböjningen med utgångspunkt från reducerat stödmoment (80%) På så sätt beaktas eftergivligheten i skarven.

Nedböjning av egentyngd:

M_ms = 0,8 · 0,620 = 0,496 kNm

\(W_{inst,q} = \frac{5}{384} \cdot \frac{{0,34 \cdot 10^3 \cdot 4,3^4
\cdot 12}}{11000 \cdot 10^6 \cdot 0,045 \cdot 0,220^3} - \frac{0,496
\cdot 10^3 \cdot 4,3^2 \cdot 12}{16 \cdot 11000 \cdot 10^6 \cdot 0,045
\cdot 0,220^3} = 0,003446 - 0,001305 = 0,002141 \: m = 2,141 \: mm \)

Nedböjning av nyttig last:

M_ms = 0,8 · 1,089 = 0,871 kNm

\(W_{inst,q} = \frac{5}{384} \cdot \frac{{0,8 \cdot 10^3 \cdot 4,3^4
\cdot 12}}{11000 \cdot 10^6 \cdot 0,045 \cdot 0,220^3} - \frac{0,871
\cdot 10^3 \cdot 4,3^2 \cdot 12}{16 \cdot 11000 \cdot 10^6 \cdot 0,045
\cdot 0,220^3} = 0,008110 - 0,002292 = 0,005818 \:m = 5,818\:mm\)

Omedelbar nedböjning

w_inst = w_inst,g + w_inst,q = 2,141 + 5,818 = 7,959 mm < 14,33 mm    OK!

Slutlig nedböjning

w_fin,g = w_inst,g (1+k_def) = 2,141 · (1 + 0,60) = 3,426 mm
w_fin,q = w_inst,q (1+ψ₂∙k_def) = 5,818 · (1 + 0,30·0,60) = 6,865 mm
w_fin = w_fin,g + w_fin,q = 3,426 + 6,865 = 10,291 mm < 14,33 mm    OK!

Sviktegenskaper

För bjälklag i bostäder med en egenfrekvens f₁ ≤ 8Hz bör en särskild utredning göras.

För bjälklag i bostäder med en egenfrekvens f₁ > 8 Hz bör följande villkor uppfyllas:

\(\frac{W}{F} \leq 1,5 \: mm/kN\)

och

\(v \leq 100^{\left(f_1 \zeta -1\right)}\:
m/(Ns^2)\)

där:
w = den maximala vertikala omedelbara utböjningen av en vertikal koncentrerad statisk kraft F,
v = bjälklagets impulshastighetsrespons, dvs den maximala vertikala initialhastigheten i m/s till följd
av en ideal stöt med storleken 1 Ns anbringad där den ger störst verkan. Från vibrationskomponenter
över 40 Hz får bortses,
ζ = relativ dämpning = 0,01 (dvs. 1 %).

Vid beräkning kan man utnyttja golvskivans förmåga att fördela lasten till angränsande golvbjälkar. Om den är spiklimmad kan man dessutom utnyttja att skiva och bjälkar samverkar statiskt vid böjning i bjälkarnas längdriktning. Kontinuitet utnyttjas inte, utan bjälken beaktas som fritt upplagd.

Samverkan mellan golvskiva och golvbjälke

Det sammansatta T-tvärsnittets böjstyvhet beräknas.

För I-balkar med tunna flänsar är effektiv flänsbredd

\(b_{ef} = b_{c,ef} + b_{w}\)

där b_c,ef = fritt avstånd mellan bjälkarna och b_w =flänsbredd

dock maximalt

b_ef = 0,2·L = 0,2·4300=860 mm på grund av skjuvdeformationer

eller b_ef = 30·h_f = 30·22=660 mm på grund av skivbuckling.
\(b_{ef} = b_{c,ef} + b_{w} = (400 -
45) + 45 = 400 \:\text{mm} \)  OK!

När man beräknar det sammansatta tvärsnittets böjstyvhet, reducerar man skivans bredd ytterligare så att den får samma tryckstyvhet som en skiva av massivt trä. Tröghetsmomentet beräknas därefter som för ett homogent tvärsnitt.

Med golvbjälkarnas E-modul E_trä = 11000 MPa och skivans E-modul vid tryck E_spån = 2200 MPa blir tryckflänsens fiktiva bredd

\(b_{m} = \frac{E_{spån}}{E_{trä}}
\cdot b_{ef} = \frac{2200}{11000} \cdot
400 = 80,0 \:\text{mm} \)

Avståndet från golvbjälkarnas underkant till neutrallagret blir 

\(x = \frac{80,0 \cdot 22 \cdot
\left(220+\frac{22}{2}\right) + 45
\cdot (\frac{220^2}{2})}{80,0 \cdot 22
+ 45 \cdot 220} = 128,26 \:\text{mm} \)

och det fiktiva tröghetsmomentet

\(I_x = \frac{45 \cdot 220^3}{12} + 45 \cdot 220 \cdot
\left( \frac{220}{2} - 128,26 \right)^2 + \frac{80,0 \cdot 22^3}{12}
+ 80,0 \cdot 22 \cdot \left( 220 + \frac{22}{2} - 128,26 \right)^2 =
61,88 \cdot 10^6 \:\text{mm}^4\)

Böjstyvhet och nedböjning

E_trä · I_x  = 11000 · 61,88·10⁶ = 68,1·10¹⁰ Nmm²

Nedböjning under punktlast 1 kN=1000 N placerad i fältmitt

\(w=\frac{F \cdot l^3}{48 \cdot
E_{trä} \cdot I_x} =
\frac{1000*4300^3}{48 \cdot 68,1 \cdot
10^{10}} = 2,43 \: \text{mm} > 1,5 \:
\text{mm} \)

Lastfördelning till angränsande golvbjälkar

När en golvbjälke böjer ned under påverkan av till exempel en punktlast tvingar golvskivan även angränsande bjälkar att följa med i rörelsen och avlastar därigenom den belastade bjälken. Denna lastfördelande effekt kan beräknas med en approximativ metod.

\(w = \frac{k \cdot F \cdot l^3}{48
\cdot E_{trä} \cdot I_x}\)

Lastfördelningsfaktorn κ (< 1) beräknas enligt ekvationen

\(k = \begin{cases}
-4,7\cdot \beta^2 + 2,9 \cdot \beta +
0,4 \qquad &0 \leqq \beta \leqq 0,3 \\
0,8 + 0,2 \cdot \beta \qquad &0,3
\leqq \beta \leqq 1
\end{cases} \)

där parametern β beskriver förhållandet mellan bjälklagets styvhet vid böjning parallellt med bjälkarna och tvärs dessa.

\(\frac{E_{trä} \cdot I_x}{s} =
\frac{68,1 \cdot 10^{10}}{400}=1702,5
\cdot 10^6 \: Nmm^2 / mm\)

Böjstyvheten tvärs balkriktningen blir (med golvspånskivans elasticitetsmodul vid böjning = 3000 N/mm²) per breddenhet

\(\frac{E_{spån} \cdot t^3}{12} =
\frac{3000 \cdot 22^{3}}{12}=2,66 \cdot
10^6 \: Nmm^2 / mm\)

\(\beta = \frac{\frac{E_{trä} \cdot I_x}{s}}{\frac{E_{spån} \cdot
t^3}{12}} \cdot \left(\frac{s}{l}\right)^4 = \frac{1702,5 \cdot
10^6}{2,66 \cdot 10^6} \cdot \left(\frac{400}{4300}\right)^4 =
0,04793 \)

Lastfördelningsfaktorn κ blir

\(-4,7 \cdot 0,04793^2 + 2,9 \cdot 0,04793 + 0,4 = 0,528\)

Nedböjning under punktlast 1 kN=1000 N placerad i fältmitt

Nedböjningen med hänsyn till både samverkan och lastfördelning blir

\(w = \frac{0,528 \cdot 1000 \cdot
4300^3}{48 \cdot 86,1 \cdot
10^{10}} = 1,28 \:\text{mm} \)

Dimensioneringsvillkoret w < 1,5mm är således uppfyllt.

Kontroll av respons på impulslast

Beräkning av lägsta egenfrekvens f₁

För ett rektangulärt bjälklag med måtten l x b fritt upplagt längs sina fyra sidor och med träbjälkar med
spännvidden l, kan egenfrekvensen f₁ beräknas approximativt enligt

\(f_1 = \frac{\pi}{2 \cdot l^2} \sqrt{\frac{\left(E_{tra} \cdot
\frac{I_x}{s}\right)}{m}} = \frac{\pi}{2 \cdot
4,3^2}\sqrt{\frac{1,7025 \cdot 10^6}{85}} = 12,0 \:\text{Hz} > 8\:
\text{Hz}\)

där m är bjälklagets massa per ytenhet i kg/m², dvs. 0,34 kN/m/0,4 x 100 = 85 kg/ m².

Impulshastighetsresponsen

För ett rektangulärt bjälklag med måtten b × l, fritt upplagt längs sina fyra sidor, kan v skattas till

\(v = \frac{4 \cdot (0,4 + 0,6 \cdot
n_{40})}{m \cdot b \cdot l
+200}\text{m/(Ns}^2)\)

där n₄₀ representerar antalet första ordningens moder av egenfrekvenser upp till 40 Hz

Värdet på n₄₀ får beräknas som

\(n_{40} = \Bigg\{ \left( \left( \frac{40}{f_1} \right)^2 -1\right)
\cdot \left(\frac{b}{l}\right)^4 \cdot \frac{(EI)_l}{(EI)_b} \Bigg\}
^{0,25}\)

där (EI)_b bjälklagets ekvivalenta plattböjstyvhet vid böjning kring en axel parallellt bjälkarnas riktning i Nm²/m och där (EI)_b < (EI)_l som är bjälklagets ekvivalenta plattböjstyvhet vid böjning kring en axel vinkelrätt mot bjälkarnas riktning i Nm²/m.

\(n_{40} = \Bigg\{ \left( \left( \frac{40}{12,0} \right)^2 -1\right)
\cdot \left(\frac{4,3}{4,3}\right)^4 \cdot \frac{1,7025 \cdot 10^6}
{2,66 \cdot 10^3} \Bigg\} ^{0,25} = 8,97\)

\(v = \frac{4 \cdot (0,4 + 0,6 \cdot
8,97)}{85 \cdot 4,3 \cdot 4,3 + 200}
= 0,0131 \: \text{m/(Ns}^2)\)

Dämpning

\(v \leq 100^{(f_1\xi -1)} \:
\text{m/(Ns}^2)\)

För normala lätta bjälklag kan ζ antas = 1%. För bjälklag med stor spännvidd eller stor tyngd bör ζ väljas något lägre. 

\(100^{(f_1\xi -1)} = 100^{(12,0
\cdot 0,01 -1)} =0,0174\: \text{m/
(Ns}^2)>\text{V}\)

Ovanstående beräkningar visar att bjälklaget uppfyller de krav som ställs på deformationer och svikt.

För att ytterligare förbättra styvheten kan kortlingar inläggas mellan bjälkarna i en eller två rader. Kortlingar ger dock en liten försämring med avseende på såväl luftljud som stegljud.