Ett träbjälklag i ett bostadshus har en fri spännvidd av 3,7 m mellan upplagen. Stommen består av träbjälkar 45 × 220 mm med 0,4 m centrumavstånd, hållfasthetsklass C18 i klimatklass 1.
Golvbeklädnaden består av 18 mm tjock OSB/3, spikad mot bjälkarna. OSB-skivorna är orienterade med sin huvudspånriktning parallellt med träbjälkarna i detta exempel.
Golvets bredd är 4,4 m och golvets massa baserad enbart på permanent last är 35 kg/m2.
Utför en dimensioneringskontroll för att bekräfta att bjälklagets vibrationsbeteende kommer att vara acceptabelt, se Dimensionering av träkonstruktioner Del 2: Avsnitt 9.4 eller Eurokod 5: Avsnitt 7.3.
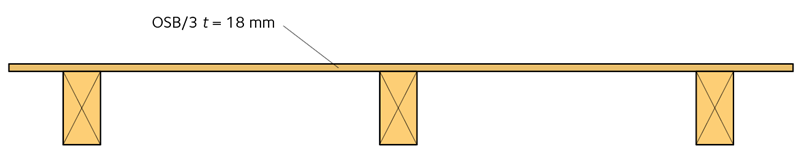
Figur 1
Tröghetsmoment I:
\({I_{\rm joist}} = \frac{{b{h^3}}}{{12}} = \frac{{0,045 \cdot {{0,22}^3}}}{{12}} = 39,93 \cdot {10^{ - 6}}{\rm{ }}{{\rm{m}}^{\rm{4}}}\)
Tröghetsmoment för golvbeklädnaden/meter bredd If :
\({I_{\mathop{\rm f}\nolimits} } = \frac{{{b_t}{t^3}}}{{12}} = \frac{{1 \cdot {{0,018}^3}}}{{12}} = 4,86 \cdot {10^{ - 7}}{\rm{ }}{{\rm{m}}^{\rm{4}}}\)
Bjälklagsstommens bredd, B = 4,4 m
Hållfasthetsklass C18
Medelvärde för elasticitetsmodulen för bjälkarna parallellt med fibrerna, E0,mean = 9 000 MPa
OSB/3
Medelvärde för elasticitetsmodulen för golvbeklädnaden, Em = 4 930 MPa
Bjälklagets massa (kg/m2), m = 35 kg/m2
a. Kontrollera lägsta egenfrekvensen för bjälklaget (se Dimensionering av träkonstruktioner Del 1: Ekvation 7.25):
\({f_1} = \frac{\pi }{{2{\ell ^2}}}\sqrt {\frac{{{{\left( {EI} \right)}_\ell }}}{m}} \)
\({f_1} = \frac{\pi }{{2 \cdot {{3,7}^2}}}\sqrt {\frac{{{{\left( {\frac{{9000 \cdot 10{}^6 \cdot 39,93 \cdot {{10}^{ - 6}}}}{{0,4}}} \right)}_{}}}}{{35}}} = 18,4\)
Den lägsta egenfrekvensen för bjälklaget är godtagbar, då den är högre än 8 Hz och ekvationerna som återfinns i Eurokod 5 kan användas för vibrationskontroll.
b. Kontrollera den statiska nedböjningen av bjälklaget enligt punktlastkriteriet i Dimensionering av träkonstruktioner Del 1: Ekvation 7.19:
Största tillåtna nedböjning är a = 1,5 mm, för en punktlast av 1 kN
\(w = \frac{{P{{\ell }^3}}}{{48EI}}\)
Kontrollera en enskild bjälke:
P = 1 000 N
\(w = \frac{{1000 \cdot {{3,7}^3}}}{{48 \cdot 9000 \cdot {{10}^6} \cdot 39,93 \cdot {{10}^{ - 6}}}} \cdot {10^3} = 2,9{\rm{\,mm}}\)
Då detta inte är tillräckligt bra, utförs en kontroll avseende effekten av styvheten i bjälklagets båda riktningar (se Dimensionering av träkonstruktioner Del 1: Ekvation 7.20 – 7.22):
\(w = \kappa \frac{{P{{\ell }^3}}}{{48EI}}\)
där lastfördelningsfaktorn κ bestäms genom:
\(\kappa = \left\{ \begin{array}{l} - 4,7{\beta ^2} + 2,9\beta + 0,4 & {\rm{då\quad }}0 \le \beta <0,3\\ 0,8 + 0,2\beta & {\rm{då\quad }}0,3 \le \beta \le 1,0 \end{array} \right.\)
med:
\(\beta = \frac{{{{\left( {EI} \right)}_\ell }}}{{\left( {EI} \right){}_{\mathop{\rm B}\nolimits} }}{\left( {\frac{s}{{\ell }}} \right)^4}\)
\(\beta = \frac{{\left( {\frac{{9000 \cdot 39,93}}{{0,4}}} \right)}}{{\left( {4930 \cdot 0,486} \right)}}{\left( {\frac{{400}}{{3700}}} \right)^4} = 0,051\)
\(\kappa = - 4,7 \cdot {0,051^2} + 2,9 \cdot 0,051 + 0,4 = 0,53\)
Vi får då, efter lastfördelning via golvskivan, en nedböjning av punktlasten:
w = 0,53 ∙ 2,9 mm = 1,6 mm
Detta innebär att den statiska verifieringen inte är helt uppfylld, men vi går ändå vidare med kontrollen. Vi skulle även kunna ändra virkeskvaliteten.
Det följande bör också gälla:
\(v \le {b^{\left( {{f_1}\zeta - 1} \right)}}\)
där v är hastighetsresponsen på enhetsimpuls (m / (Ns2). ζ är den relativa dämpningen, vilken normalt kan sättas till 0,01. Konstanten b för kontroll av hastighetsresponsen på enhetsimpuls kan sättas till 100 (se Dimensionering av träkonstruktioner Del 2: Avsnitt 9.4):
\(v \le {b^{\left( {{f_1}\zeta - 1} \right)}} = {100^{\left( {18,4 \cdot 0,01 - 1} \right)}} = 0,023\)
Hastighetsresponsen på enhetsimpuls erhålls genom:
\(v = \frac{{4\left( {0,4 + 0,6{n_{40}}} \right)}}{{mB{\ell } + 200}}\)
där n40 är antalet moder av första ordningen, med egenfrekvenser upp till 40 Hz och B är bjälklagsbredden. Värdet av n40 kan beräknas ur:
\({n_{40}} = {\left\{ {\left( {{{\left( {\frac{{40}}{{{f_1}}}} \right)}^2} - 1} \right){{\left( {\frac{B}{{\ell }}} \right)}^4}\frac{{\left( {EI} \right){}_\ell }}{{{{\left( {EI} \right)}_{\mathop{\rm B}\nolimits} }}}} \right\}^{0,25}}\)
\({n_{40}} = {\left\{ {\left( {{{\left( {\frac{{40}}{{18,4}}} \right)}^2} - 1} \right){{\left( {\frac{{4400}}{{3700}}} \right)}^4}\frac{{\left( {\frac{{9900 \cdot 39,93}}{{0,4}}} \right)}}{{\left( {4930 \cdot 0,486} \right)}}} \right\}^{0,25}} = 7,5\)
Hastighetsresponsen på enhetsimpuls blir då:
\(v = \frac{{4\left( {0,4 + 0,6 \cdot 7,5} \right)}}{{35 \cdot 4,4 \cdot 3,7 + 200}} = 0,025\)
Detta värde är högre än gränsvärdet 0,023 m / (Ns2). Den valda bjälklagsuppbyggnaden bör därför justeras för att undvika problem med vibrationer.

