För saknad information, se beräkningsexemplet Dimensionering av en sadelbalk (ULS och SLS).
Stomgeometri:
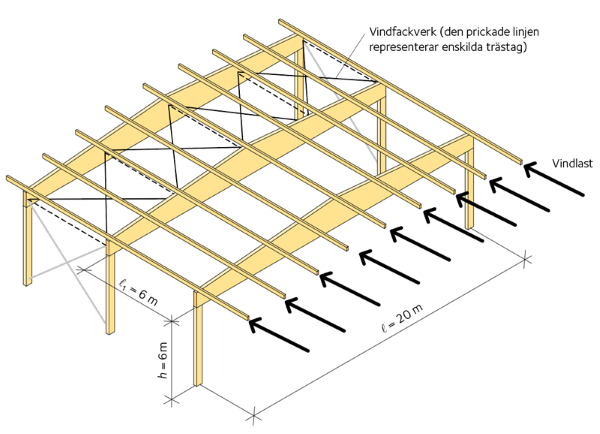
Byggnaden med dimensionerna ℓ × ℓtot 20 × 36 m stagas med hjälp av ett vindfackverk i taket, bestående av diagonala stålstänger och tryckstag av limträ i byggnadens längdriktning. Vindfackverket placeras rakt under takytan. De horisontella lasterna leds in via takåsarna och tas upp av separata tryckstag, vilka ligger i samma plan som de diagonala stålstängerna. Detta för att undvika excentriciteter i fackverksknutpunkterna. Upplagsreaktionerna från vindfackverket leds via vindkryss av stålstänger i långsideväggarna ner till grundkonstruktionen, men de dimensioneras inte i detta exempel. Stomgeometrin visas i Figur 1 nedan:
Figur 1
Laster som verkar på vindfackverket
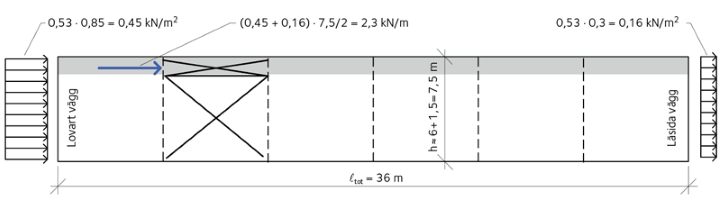
Lasterna som beaktas vid dimensioneringen av takets vindfackverk är följande: vind som primär last och böjtröghetseffekter orsakade av balkens egentyngd, takets egentyngd samt snö. Det karakteristiska värdet för vindlast antas vara 0,53 kN/m3, vilket ger upphov till ett tryck på väggen på byggnadens lovartsida och sug på väggen på läsidan av byggnaden. Formfaktorn sätts till 0,85 och 0,3 för väggen på lovartsidan respektive läsidan. Vindlasterna som beaktas vid dimensioneringen av takets vindfackverk visas i Figur 2.
Figur 2
Tabell 1
| Lasttyp | Jämnt utbredd last [kN/m2] |
Jämnt utbredd last [kN/m] |
Lastkombinationsfaktor ψ0 |
| Vind | 0,45 + 0,16 = 0,61 | wk = 0,61 ⋅ 7,5 / 2 = 2,3 | 0,3 |
| Balkens egentyngd | – | g1k = 1,10 | – |
| Takets egentyngd | 0,6 | g2k = 3,96 | – |
| Snö | 1,5 | s = 8,77 | 0,6 |
Förutom vind ska lasten genererad av primärbalkarnas avvikelse från rakt tillstånd (andra ordningens effekter) beaktas. Denna last kan betraktas som jämnt utbredd och dess karakteristiska värde kan beräknas enligt Dimensionering av träkonstruktioner Del 1: Ekvation 6.28:
\({q_\rm h} = n \cdot \frac{M}{{30h \cdot {\ell }}} \cdot \left( {1 - {k_{\rm crit}}} \right)\)
där:
- n = 6 är antalet stagade balkar (notera att det totala antalet balkar är 7, men balkarna vid de två gavlarna bär endast halva den vertikala lasten).
- M är böjmomentet i balken på grund av vertikala laster, vid beaktande av lastkombinationen ”STR B” enligt Eurokod 0. Lastkombinationsfaktorn bör anges ψ0 = 0,6 då vindlast betraktas som huvudlast och ψ0 = 1,0 då snö betraktas som huvudlast:
- ℓ = 20 m \(M = \frac{{q{{\ell }^2}}}{8} = \frac{{\left[ {1,2 \cdot \left( {{g_{\rm 1,k}} + {g_{\rm 2,k}}} \right) + 1,5 \cdot {\psi _0} \cdot s} \right] \cdot {{\ell }^2}}}{8}\)
- kcrit är faktorn som tar hänsyn till risken för vippning av en icke stagad balk. Höjden på balken kan anges till hm = (h + hap) / 2 ≈ 1 200 mm och ℓef = 0,9 · ℓ + 2h:
\({\lambda _{\rm rel,m}} = \sqrt {\frac{{{f_{\rm m,k}}}}{{{\sigma _{\rm m,crit}}}}} = \sqrt {{f_{\rm m,k}} \cdot \frac{{h \cdot {\ell _{{\mathop{\rm ef}\nolimits} }}}}{{0,78 \cdot {b^2} \cdot {E_{0,05}}}}} \) - kcrit = se Dimensionering av träkonstruktioner Del 1: Tabell 3.3
I detta exempel beaktas inte pelarnas snedställningslast. För mer information se Projektering av limträkonstruktioner.
Tabell 2
| Lastkombination | Böjmoment i balken M [kNm] | λrel,m | kcrit | qh [kN/m] |
| a) Vind är huvudlast |
\(\frac{{\left[ {1,2 \cdot \left( {1,1 + 3,96} \right) + 0,6 \cdot 1,5 \cdot 8,77} \right] \cdot {{20}^2}}}{8} = 698,5\) |
1,55 | 0,41 | 3,4 |
| b) Snö är huvudlast |
\(\frac{{\left[ {1,2 \cdot \left( {1,1 + 3,96} \right) + 1,5 \cdot 8,77} \right] \cdot {{20}^2}}}{8} = 961,5\) |
1,55 | 0,41 | 4,7 |
Lastkombinationer
Säkerhetsklassen antas vara hög (säkerhetsklass 3), således är γd = 1. Balkarna antas vara placerade inomhus, i en uppvärmd miljö. Därför karakteriseras de av en miljö där den relativa fuktigheten mycket sällan, om alls, överstiger 65 %. Alltså kan klimatklassen sättas till 1. I detta exempel beaktas endast lastkombination i brottgränstillstånd. Endast lastkombinationen med vind som huvudlast visas här.
Tabell 3
| Säkerhetsklass | Klimatklass | Lastkombinationer [kN/m] | Lastvaraktighet | kmod |
| 3 → γd = 1 | 1 | a) qd,a = 1 ⋅ [1,5 ⋅ wk + 1,0 ⋅ qh] = =1,5 ⋅ 2,3 + 3,4 = 6,9 |
kort | 0,9 |
| 3 → γd = 1 | 1 | b) qd,b = 1 ⋅ [1,0 ⋅ qh + 1,5 ψ0,w wk] = =1,0 ⋅ 3,4 + 1,5 ⋅ 0,3 ⋅ 2,3 = 4,5 |
medellång | 0,8 |
Den styrande lastkombinationen är alltså a), det vill säga vind som huvudlast.
Material
1. Träelement
Materialet som används för stagen är limträ GL30c (γM = 1,25, kmod = 0,9). Det antagna tvärsnittet för staget är 190 × 180 mm. Över- och underramen i vindfackverket är två bredvid varandra liggande sadelbalkar. Balkarnas tvärsnittshöjd varierar längs spannet från 700 mm vid upplagen till 1 698 mm mitt på spannet. För enkelhetens skull kan det emellertid antas att balkarna har ett konstant tvärsnitt 190 × 1 200 mm2. Även balkarna är tillverkade av limträ GL30c. Relevanta dimensioneringsvärden visas nedan:
Tabell 4
| Dimensioneringsvärden | |
| Tryck parallellt med fibrerna | fc,0,d = 17,6 MPa |
| Drag parallellt med fibrerna | ft,0,d = 14,0 MPa |
| Elasticitetsmodul | E0,mean = 13 000 MPa E0,05 = 10 800 MPa |
2. Ståldiagonaler
Diagonalerna består av stålstänger, kvalitet 4.8. Stängerna är gängade i ändarna.
Tabell 5
| Typ av stång | Dimensionerande böjspänning fyb [MPa] |
Dimensionerande brottspänning fub [MPa] |
| Stål 4.8 | 320 | 400 |
Dimensionering av vindfackverket
Vindfackverket består av:
- underram och överram av limträ
- ortogonala tryckstag av limträ
- diagonalstänger av stål.
Statiskt system
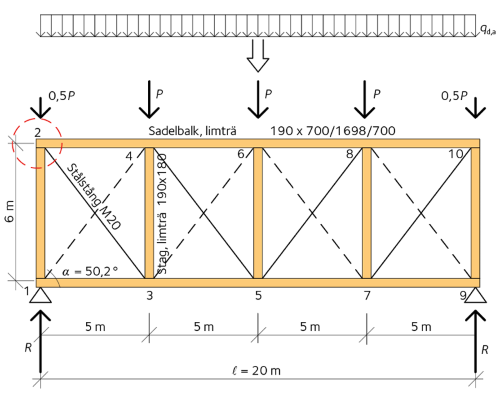
Figur 3
Krafter verkande på systemet
\(P = \frac{{{q_{\rm d,a}} \cdot \ell }}{4} = \frac{{6,9 \cdot 20}}{4} = 34,5\;{\rm{kN}}\)
\(R = \frac{{4 \cdot P}}{2} = \frac{{4 \cdot 34,5}}{2} = {69,0_{}}{\rm{\,kN}}\)
a. Tryckstag
De mest belastade stagen är de vid upplagen (det vill säga stag 1 – 2 och 9 – 10). Kraften som verkar i dessa stag är:
\({N_{\rm sd}} = {N_{1 - 2}} = {N_{9 - 10}} = R = {69,0_{}}{\rm{\,kN}}\)
Tabell 6
| Tvärsnitt | Relativ slankhet \({\lambda _{\rm rel}} = \frac{\lambda }{\pi }\sqrt {\frac{{{f_{{\mathop{\rm ck}\nolimits} }}}}{{{E_{0,05}}}}} \) |
Reduktions- faktor kc |
Tryckkraft i staget Nsd [kN] |
Tryckhållfasthet för staget NRd [kN] |
Utnyttjande- grad |
| 190 x 180 | 1,695 | 0,348 | 69,0 | kc ⋅ A ⋅ fc,d = 0,348 ⋅ 0,19 ⋅ 0,18 ⋅17,64 ⋅ 103 = 210 kN |
69,0 / 210 = 0,33 |
Samma tvärsnitt, det vill säga 190 × 180 mm antas för alla stag i vindfackverket.
b. Diagonala stålstänger
De mest belastade ståldiagonalerna är de vid upplagen (det vill säga diagonalerna 2 – 3 och 7 – 10). Kraften som verkar i dessa diagonaler är:
Grafisk representation av krafterna som verkar i nod 2
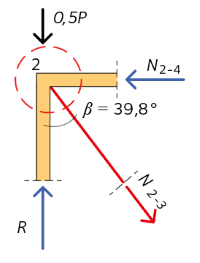
Figur 4
Krafter verkande i stålstången
\(\begin{array}{l} {N_{\rm sd}} = {N_{2 - 3}} = \left( {R - \frac{P}{2}} \right)\frac{1}{{\cos \beta }} = \left( {69,0 - \frac{{34,5}}{2}} \right) \cdot \frac{1}{{\cos {{39,8}^{\rm{o}}}}} = {67,4_{}}{\rm{\,kN}} \end{array}\)
Kraften som verkar i den diagonala stålstången är Nsd = 67,4 kN. Dimensioneringen av de diagonala stålstängerna utförs som om de vore bultar utsatta för dragkraft, eftersom ändarna av stålstängerna är gängade. Partialkoefficienten för bultar är γM2 = 1,2.
Tabell 7
| Stålkvalitet | Dimension | Spänningsarea As [mm2] |
Brottspänning fub [MPa] |
Dragspänning i stången \({F_{\rm t,Rd}} = 0,9 \cdot \frac{{{f_{\rm ub}} \cdot {A_\rm s}}}{{{\gamma _{\rm M2}}}}\left[ {{\rm{kN}}} \right]\) |
| 4.8 | M12 | 84 | 400 | 25,2 |
| 4.8 | M16 | 157 | 400 | 47,1 |
| 4.8 | M20 | 245 | 400 | 73,5 |
| 4.8 | M24 | 353 | 400 | 105,9 |
- Stålstång M20, 4.8 väljs som diagonala element i vindfackverket.
\({N_{\rm sd}} = 67,4\;{\rm{kN}}<{F_{\rm t,Rd}} = 73,5\;{\rm{kN}}\) → OK