Kontroll av pelare för brand

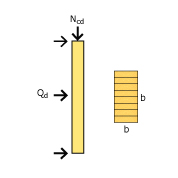
Bild 1.

1. Förutsättningar

• Pelaren är ledat infäst i båda ändar (pendelpelare)
• Pelarens dimensioner: 165 x 360 mm²; L = 7 000 mm, L40 c 
• Byggnadens bredd: B = 30 000 mm
• Snölastens karakteristiska lastvärde: s_k = 2,0 kN/m²; ψ₀ = 0,7
• Egentyngd av takbeläggning, takbalkar och takåsar: g_k = 0,55 kN/m²
• Vindlastens karakteristiska lastvärde: q_k = 0,49 kN/m²; ψ = 0,25
• Säkerhetsklass 3, γ_d=1,0
• Klimatklass 1
• Centrumavstånd mellan takbalkar och pelare: S_T = 7 200 mm

Byggnaden hänförs till brandklass Br2.

2. Kontroll av brandlastfallet

Brandkontroll utförs enligt beräkningsmodellen i eurokoder. De dimensionerande lasterna beräknas enligt lastkombination för olyckslast, ekvation 6.11 a/b.

\(q_d = \gamma_d \cdot G_k + \gamma_d \cdot \psi_{1,1} \cdot Q_{k1} + \gamma_d \cdot \sum\psi_{2,i} \cdot Q_{k,i}\)

Vid brand uppkommer det termiska laster. Den termiska delen tar hänsyn till tvång i samband med temperaturrörelser och är därför inte aktuellt för konstruktionsdelar i trä. Dock så bör det observeras att då förband med ståldetaljer används kan tvång uppkomma.

3. Beräkning av lasteffekter

Pelaren kommer att belastas med både moment på grund av vind på vägg och tryckande normalkraft som uppstår av last, snö och egentyngd, från taket.

Beräkning av dimensionerande moment

Dimensionerande last av vind på vägg beräknas som

\(q_d = 1,0 \cdot \psi_{1,1} \cdot q_k \cdot s_r = 1,0 \cdot 0,2 \cdot 0,49 \cdot 7,2 = 0,71 \:\text{kN/m} \)

Dimensionerande lasteffekt av moment i mittsnittet

\(M_{sd}=\frac{q_d \cdot l^2}{8}=\frac{0,71 \cdot 7,0^2}{8} = 4,3 \:\text{kN/m}\)

Beräkning av dimensionerande normalkraft

Dimensionerande vertikal last av snölast och egenvikter beräknas som 

\(q_{d,dim}=(1,0 \cdot g_k + 1,0\cdot \psi_{1,1}\cdot s_k)\cdot s_r = (1,0 \cdot 0,55 + 1,0 \cdot 0,4 \cdot 2,0)\cdot 7,2 = 9,7\:\text{kN/m}\)

Reducerad vertikal last av snölast och egenvikt beräknas som 

\(q_{d,red}=(1,0 \cdot g_k + 1,0\cdot \psi_{2,1}\cdot s_k)\cdot s_r = (1,0 \cdot 0,55 + 1,0 \cdot 0,2 \cdot 2,0)\cdot 7,2 = 6,8\:\text{kN/m}\)

Vid antagande om att takbalkarna kan betraktas som fritt upplagda på pelaren fås dimensionerande normalkraft som

\(N_{Sd}=\frac{q_d \cdot B}{2}=\frac{9,7 \cdot 30,0}{2}=146\:\text{kN}\)

\(N_{Sd,rel}=\frac{q_d \cdot B}{2}=\frac{6,8 \cdot 30,0}{2}=102\:\text{kN}\)

4. Kontroll av pelare i brandlastfallet

Kontrollen utförs enligt metoden given i Eurokod 5. Metoden beaktar brand genom en reducering av tvärsnittet och en reduktion av styvhets- och hållfasthetsvärden.

Beräkning av resttvärsnitt

Pelaren utsätts för tresidig brandbelastning.

Bild 2.

Det effektiva inbränningsdjupet beräknas som

d_ef = d_char + d₀

där d_char är faktiskt inbränningsdjup och d₀ beaktar avrundade hörn.  Avrundade hörn beaktas genom en ökning av inbränningsdjupet. d_ef = d_char = β_n · t

β_n = 0,7 mm/min (inbränningshastighet för limträ, inkluderat effekten av hörn och sprickor)

För pelare i brandklass Br2 gäller kravet R30 för bärförmågan, det vill säga bärförmågan ska säkerställas under 30 min.

d_ef = d_char = β_n · t = 0,7 · 30 = 21 mm

Nya dimensioner för pelaren blir, b_rest = 165 - 2 · 21 = 123 mm och h_rest = 360 - 21 = 339 mm. Pelarens dimension med hänsyn till tresidig inbränning blir 123x339 mm².

Beräkning av reducerade styvhets- och hållfasthetsvärden

Reducerade styvhets- och hållfasthetsvärden beräknas enligt

\(f_{fi,d}=k_{mod,fi}\cdot \frac{k_{fi}\cdot f_k}{\gamma_{m,fi}\cdot \gamma_{n,fi}}\)

\(\gamma_{m,fi}=\lambda_{n,fi}=1,0\)

\(k_{fi}= 1,15\)

\(k_{mod,fi}= 1,0 -k \cdot \frac{P}{A_{rest}}\)

där k = 0,008 för tryckhållfastheten,k = 0,005 för böjhållfastheten och k = 0,003 för elasticitetsmodulen. Parametern ρ betecknar den brandexponerade delen av resttvärsnittets omkrets i meter. A_rest är resttvärsnittets area i m². 

\(k^c_{mod,fi}=1,0 - 0,008 \cdot \frac{2 \cdot 0,339 + 0,123}{0,123 \cdot 0,339}=0,85\)

\(k^m_{mod,fi}=1,0 - 0,005 \cdot \frac{2 \cdot 0,339 + 0,123}{0,123 \cdot 0,339}=0,90\)

\(k^e_{mod,fi}=1,0 - 0,003 \cdot \frac{2 \cdot 0,339 + 0,123}{0,123 \cdot 0,339}=0,94\)

De karakteristiska hållfastheterna i böjning (f_mk = 30,8 MPa) och tryck (f_ck = 25,4 MPa) parallellt fibrerna bestäms enligt anvisningar för limträ (L40 c) med klimatklass 2.
Dimensionerande moment- och tryckhållfasthet kan nu beräknas som

\(f^c_{fi,d}=0,85 \cdot \frac{1,15 \cdot 25,4}{1,0 \cdot 1,0} = 24,8 \:\text{MPa}\)

\(f^m_{fi,d}=0,90 \cdot \frac{1,15 \cdot 30,8}{1,0 \cdot 1,0} = 31,9 \:\text{MPa}\)

\(E_{fi,d}=0,94 \cdot \frac{1,15 \cdot 10500}{1,0 \cdot 1,0} = 11378 \:\text{MPa}\)

Beräkning av bärförmåga i böjning

Bärförmågan i böjning beräknas som

\(M_{Rd} = \kappa_{inst} \cdot f^m_{fi,d}\cdot W\)

Antag att pelaren är förhindrad av fasaden att vippa κ_inst = 1,0. Oftast består fasaden i hallbyggnader av väggåsar med skivmaterial utanpå. Väggåsarna och skivmaterialet kan tillsammans med pelarna anses skapa en styv skiva som förhindrar vippningen i fasadens plan.

\(M_{Rd} = 1,0 \cdot 31,9 \cdot 10^6 \cdot \frac{0,123 \cdot 0,339^2}{6} = 75,2 \:\text{kNm}\)

Beräkning av bärförmåga i tryck

Bärförmågan i tryck beräknas som

\(N_{Rd}=\kappa_{cr} \cdot f^c_{fi,d}\cdot A\)

Antag att pelaren är förhindrad att knäcka i vek riktning av fasaden. På samma vis som vid vippning så kan väggåsarna och skivmaterialet i fasaden anses skapa en styv skiva som förhindrar knäckning i fasadens plan. Risken för knäckning beaktas genom slankhetstalet för knäckning i pelarens styva riktning 

\(\lambda_c = \frac{l_c}{i} = \frac{l_c}{\sqrt{\frac{I}{A}}} = \frac{l_c \cdot \sqrt{12}}{h} = \frac{7,0 \cdot \sqrt{12}}{0,339} = 71,5 \)

\(\lambda_r = \frac{\lambda_c}{\pi} \cdot \sqrt{\frac{f^c_{fi,d}}{E_{fi,d}}} = \frac{71,5}{\pi} \cdot \sqrt{\frac{24,8}{11378}}=1,06\)

\(k = 0,5 \cdot \left(1 + \beta \cdot (\lambda_r - 0,5)+{\lambda_r}^2 \right) = 0,5 \cdot \left(1 + 0,1 \cdot ( 1,06 - 0,5) + 1,06^2\right)=1,09\)

\(\kappa_{cr} = \frac{1}{k + \sqrt{k^2 - {\lambda_r}^2}} = \frac{1}{1,09 + \sqrt{1,09^2 - 1,06^2}} = 0,74\)

Bärförmågan i tryck kan nu beräknas

\(N_{Rd} = \kappa_{cr} \cdot f^c_{fi,d} \cdot A =0,55 \cdot 24,8 \cdot 10^6 \cdot 0,123 \cdot 0,339 = 769 \:\text{kN}\)

Kontroll av dimensioneringsvillkor

Vind som huvudlast ger

\(\frac{M_{Sd}}{M_{Rd}} + \frac{N_{Sd}}{N_{Rd}} = \frac{4,3}{75,2} + \frac{102}{769} = 0,19 < 1,0\)

Snö som huvudlast

\(\frac{M_{Sd}}{M_{Rd}} + \frac{N_{Sd}}{N_{Rd}} = \frac{0}{75,2} + \frac{146}{769} = 0,19 < 1,0\)

Dimensioneringsvillkoret är uppfyllt!