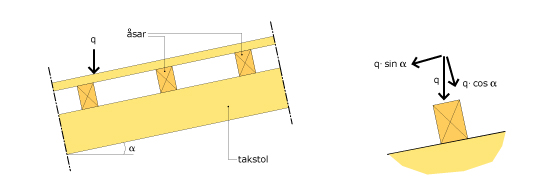
Bild 1.
1. Förutsättningar
Taklutning: α = 14° < 30°
Snölastens karakteristiska lastvärde: sk = 2,5 kN/m2
Snölastens formfaktor: µ = 0,8, Lastvaraktighetsklass medel (M)
Egentyngd av takbeläggning och takåsar: gk = 0,40 kN/m2
Säkerhetsklass: 2 (γd = 0,91)
Klimatklass: 2
Centrumavstånd mellan takbalkar: sT = 7 200 mm
Centrumavstånd mellan takåsar: sÅ = 2 400 mm
2. Preliminär dimensionering
Preliminär dimension för takåsarna bestäms enligt Limträhandboken. För en rak kontinuerlig balk upplagd över flera stöd rekommenderas en minsta höjd av L/20 = 7 200/20 = 360 mm, bredden väljs till 78 mm. Som preliminär dimension för takåsarna av limträ väljs dimensionen 90x360 mm2 i kvalitet CE L40c.
3. Kontroll av brottgränstillståndet
Lasteffekter
Säkerheten mot brott kontrolleras för lastfallet med snö och egentyngd då snö är huvudlast Dimensionerande lastvärde blir
\(\bar{q}_d=0,91 \cdot 0,89 \cdot 1,35 \cdot g_k + \gamma_d \cdot 1,5
\cdot \mu \cdot s_k = 0,91 \cdot 0,89 \cdot 1,35 \cdot 0,40 + 0,91
\cdot1,5 \cdot 0,8 \cdot 2,5 = 3,16 \:\text{kN/m}^2\)
Varje takås kommer att belastas med linjelasten
\(q_d = \bar{q}_d \cdot s_{\text{Å}}= 3,16\cdot 2,4 = 7,58 \:\text{kN/m}\)
Då takets lutning överstiger 1:10 måste, enligt Limträhandboken, sned böjning för takåsarna beaktas. Linjelasten på takåsen komposantuppdelas i två linjelaster verkande i x-led och y-led.
\({q_d}^y=q_d \cdot \sin\alpha = 7,58 \cdot \sin14^\circ = 1,83 \:\text{kN/m}\)
\({q_d}^z=q_d \cdot \cos\alpha = 7,58 \cdot \cos14^\circ = 7,35 \:\text{kN/m}\)
Dimensionerande moment i ytterfack för ett omlottskarvat åssystem kan beräknas enligt Limträhandboken.
\(M_{y,d} = 0,080 \cdot {q_d}^z \cdot {s_\text{T}}^2 = 0,080 \cdot 7,35 \cdot
{7,2}^2 = 30,5 \:\text{kNm}\)
\(M_{z,d} = 0,080 \cdot {q_d}^z \cdot {s_\text{T}}^2 = 0,080 \cdot 1,83 \cdot
{7,2}^2 = 7,6 \:\text{kNm}\)
I innerfack för en kontinuerligt omlottskarvad ås gäller enligt Limträhandboken
\(M_{y,d} = 0,046 \cdot {q_d}^z \cdot {s_\text{T}}^2 = 0,046 \cdot 7,40 \cdot {7,2}^2
= 17,5 \:\text{kNm}\)
\(M_{z,d} = 0,046 \cdot {q_d}^z \cdot {s_\text{T}}^2 = 0,046 \cdot 1,83 \cdot {7,2}^2
= 4,4 \:\text{kNm}\)
I detta fall dimensioneras hela åsen för momentet i ytterfacket. Alternativt kan systemet anordnas med olika dimensioner i ytter- och innerfack, oftast anordnas då åsarna med samma höjd i alla fack. redden i ytterfacken måste då ökas för att uppta det större momentet.
\(\sigma_{m,y,d} = \frac{M_{y,d}}{W} = \frac{30,5 \cdot 10^6 \cdot 6}{90 \cdot 360^2} = 15,7 \:
\text{MPa}\)
\(\sigma_{m,z,d} = \frac{M_{z,d}}{W} = \frac{7,6 \cdot 10^6 \cdot 6}{360 \cdot 90^2} = 15,6 \:
\text{MPa}\)
Bärförmåga
Takbeläggningen antas i detta fall vara nog styv för att avstyva takåsen så att vippning kan förhindras, kcrit = 1,0. Den dimensionerande hållfastheten i böjning beräknas för materialet Limträ (CE L40c), klimatklass 2 och lastvaraktighetsklass medel. Eftersom tvärsnittets höjd är < 600 mm får man även öka bärförmågan i böjning på grund av storlekseffekter.
Dimensionerande värde på böjhållfastheten beräknas.
fmk = 30,8 MPa (CE L40c)
kmod = 0,8 (lastvaraktighet medel, klimatklass 2)
γm = 1,25 (limträ)
\({\kappa_h}^y = min \begin{cases} \left( \frac{600}{h} \right)^{0,1} = \left(\frac{600}
{360} \right)^{0,1} = 1,05 \\ 1,1 \end{cases}\) (Höjd = 360 mm)
\({\kappa_h}^z = min \begin{cases} \left( \frac{600}{h} \right)^{0,1} = \left(\frac{600}{90}
\right)^{0,1} = 1,21 \\ 1,1 \end{cases}\) (Höjd = 78 mm)
Dimensionerande bärförmåga i böjning i respektive riktning kan nu beräknas som
\(f_{m,y,d} = {\kappa_h}^y \cdot \frac{k_{mod} \cdot f_{mk}}{\gamma_m} = 1,05 \cdot
\frac{0,8 \cdot 30,8}{1,25} = 20,7 \:\text{MPa}\)
\(f_{m,z,d} = {\kappa_h}^x \cdot \frac{k_{mod} \cdot f_{mk}}{\gamma_m} = 1,1 \cdot
\frac{0,8 \cdot 30,8}{1,25} = 21,7 \:\text{MPa}\)
Säkerheten mot brott kontrolleras med dimensioneringsvillkoren
\(\left(\frac{\sigma_{m,y,d}}{f_{m,y,d}}\right) + 0,7 \cdot
\left(\frac{\sigma_{m,z,d}}{f_{m,z,d}}\right) \leq 1,0\)
\(0,7 \cdot \left(\frac{\sigma_{m,y,d}}{f_{m,y,d}}\right) +
\left(\frac{\sigma_{m,z,d}}{f_{m,z,d}}\right) \leq 1,0\)
Med insatta värden fås
\(\left(\frac{15,7}{20,7}\right) + 0,7 \cdot \left(\frac{15,6}{21,7}\right) = 1,26 >
1,0\)
\(0,7 \cdot \left(\frac{15,7}{20,7}\right) + \left(\frac{15,6}{21,7}\right) = 1,25 >
1,0\)
Villkoret för säkerhet är ej uppfyllt!
För att minska den last som påförs i åsen veka riktning (z-led) kan dragband anordnas som därvid fungerar som ett upplag.
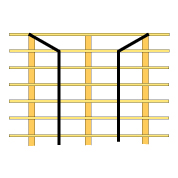
Bild 2.
Om vi anordnar ett dragband mitt i facket kommer det maximala momentet i z-led att reduceras till
\(M_{z,d}=0,08 \cdot 1,83 \cdot \left(\frac{7,2}{2} \right)^2 = 1,89 \:\text{kNm} \)
\(\sigma_{m,z,d}= \frac{M_{z,d}}{W}= \frac{1,89 \cdot 10^6 6}{360 \cdot 90^2} =3,89 \:\text{kNm}\)
Dimensioneringsvillkoren ger nu
\(\left( \frac{15,7}{20,7} \right) + 0,7 \cdot\left(\frac{3,89}{21,7} \right) = 0,88 < 1,0\)
\(0,7 \cdot \left( \frac{15,7}{20,7} \right) + \left(\frac{3,89}{21,7} \right) = 0,71 < 1,0\)
Villkoret för säkerhet är nu uppfyllt!
Observera att dragbandet måste dimensioneras för ett krafttillskott från samtliga åsar, i detta fall skulle vi erhålla följande kraft i dragbandet
\( N_{Sd} = {q_d}^z \cdot \frac{L}{2} \cdot n \)
där n är antalet åsar som hängs upp i dragbandet. I detta fall belastar totalt 5 åsar dragbandet, här räknas med att nockåsen och kantåsen endast påverkas av en halv belastningsyta. För att undvika att nockåsen utsätts för en tillskottskraft i sin veka riktning måste en noggrann infästning av dragbandet utföras. Dragbandet ska överföra krafterna från åsarna, genom dragbandet, till takbalken, dragbandet måste därför dras förbi nocken och fästas i takbalken.
Kontroll av skjuvning
Dimensionerande tvärkraft uppträder vid takåsarnas upplag mot takbalkarna. Största tvärkraft för en kontinuerlig ås upplagd på flera stöd kan bestämmas enligt lämplig formelsamling.
\( V_{zd} = 0,6053 \cdot {q_d}^z \cdot s_T = 0,6053 \cdot 7,35 \cdot 7,2 = 32,0 \:\text{kN} \)
Skjuvspänning beräknas
\( \tau_d = \frac{1,5 \cdot V_{zd}}{A} = \frac{1,5 \cdot 32,0 \cdot 10^3}{90 \cdot 360}=1,48 \:\text{MPa}\)
Dimensionerande värde på skjuvhållfastheten blir med
fvk = 3,5 MPa (CE L40c)
kmod = 0,8 (lastvaraktighet medel, klimatklass 2)
γm = 1,25 (limträ)
Enligt allmänt råd i EKS 9, BFS 2013:10, bör kcr enligt nedan användas för limträ som inte är exponerat för nederbörd och solstrålning.
\( k_{cr} = min \begin{cases} \frac{3,0}{f_{v,k}} \\ 1,0 \end{cases} \)
\( \frac{3,0}{f_{v,k}} = \frac{3,0}{3,5} = 0,857 < 1,0 \:\text{alltså}\: k_{cr}=0,857 \)
\( f_{v,d}=\frac{k_{cr} \cdot k_{mod} \cdot f_{v,k}}{\gamma_m} = \frac{0,857 \cdot 0,8 \cdot 3,5}{1,25}
= 1,92\:\text{MPa} > 1,48 \:\text{MPa} \)
Dimensioneringsvärdet \( \tau_d < f_{v,d} \) är uppfyllt!
4. Kontroll av bruksgränstillståndet
Detta kan ske om så erfordras, se exempel Jämnhög rak balk av fanerträ.

