Balkbro för gång- och cykeltrafik

Brons spännvidd är 11 m och bredden 2 m. Den utförs som en balkbro med brobana av syllar och plank.

Dimensionering ska utföras enligt gällande regler och standarder samt beställarens anvisningar.

• Enligt Trafikverkets TRVK Bro ska träkonstruktioner dimensioneras enligt SS-EN 1995-1-1 (Eurokod 5: Del 1-1) och SS-EN 1995-2 (Eurokod 5: Del 2).
• Enligt Trafikverkets TRVR Bro hänförs vid tillämpning av klimatklasser enligt SS-EN 1995 (Eurokod 5) konstruktionsdelar av trä i en bro till klimatklass 3. Under förutsättning att de är ventilerade kan följande konstruktionsdelar dock hänföras till klimatklass 2: delar skyddade av brobaneplatta eller tak; brobaneplattor med tätskikt; delar skyddade av intäckning.
• Enligt Trafikverket (TRVFS 2011:12) bör säkerhetsklass 2 tillämpas för broar med teoretisk spännvidd högst lika med 15,0 m i största spannet. 

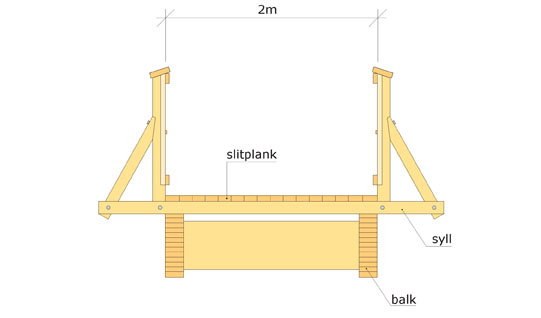
Bild 1.

Efter överslagsberäkning väljs två limträbalkar med spännvidd 11 m. Varje balk belastas med last från 1,0 m brobredd. Balkarnas dimension antas till 165x585 mm och utförs av limträ i hållfasthetsklass CE L40c.

Överslagsmässigt bestäms hur många limträbalkar som behövs och ungefärlig balkdimension. Man kan i detta fall med brobredd 2 m börja med att anta att det räcker med två balkar. Sedan antar man en dimension och beräknar egentyngden för en balk. Med dimensionen 165 mm x 585 mm får man egentyngd cirka 0,5 kN/m. Egentyngd för plankdäck och räcke antas också belasta balken med 0,5 kN/m. Trafikens ytlast antas till 5 kN/m² och dimensionerande last blir då 1,5x5=7,5 kN/m för varje balk. Totala lasten blir 8,5 kN/m för varje balk. Det ger böjmomentet cirka128 kNm och böjspänningen 13,6 MPa, vilket är lägre än dimensionerande böjhållfastheten för limträ. Det betyder att det borde räcka med två balkar och man kan börja dimensioneringen med den antagna dimensionen. Om böjspänningen däremot skulle bli för hög, så får man prova med större balkar eller med fler balkar om det finns krav på maximal höjd för bron eller om bron blir orimligt hög. För övriga komponenter kan man göra motsvarande överslagsberäkningar för att finna dimensioner att utgå från.

Som tvärbalkar väljs 90x450 mm av limträ i hållfasthetsklass CE L40c. Som syllar väljs 70x120 mm av konstruktionsvirke i hållfasthetsklass C24 och med centrumavståndet 600 mm. Spännvidden för syllarna är lika med centrumavståndet mellan balkarna, det vill säga 2 m - 0,165 m = 1,835 m. Som slitplank väljs 70x195 mm av konstruktionsvirke i hållfasthetsklass C24. Spännvidden för slitplanken är syllarnas centrumavstånd 600 mm. Som räckesstolpar väljs 70x120 mm av konstruktionsvirke i hållfasthetsklass C24 med centrumavståndet 1800 mm. Räckeshöjd är 1,4 m, och räcket utförs med snedsträva som stöd.

1. Förutsättningar

Laster enligt eurokoder

Allmänna laster - Tunghet, egentyngd, nyttig last för byggnader, SS-EN 1991-1-1:2002
Trafiklast på broar, SS-EN 1991-2:2003
Allmänna laster - Vindlast, SS-EN 1991-1-4:2005

Egentyngd

• Tunghet för limträ CE L40c är 4,0 kN/m³
• Tunghet för konstruktionsvirke C24 är 4,2 kN/m³
• Egentyngd räcke är 0,18 kN/m
• Egentyngd per limträbalk blir G_k = 0,165 · 0,585 · 4,0 (limträ) + 0,07 · 0,12 · 1,0 · 4,2 / 0,6 (syll) + 1,0 · 0,07 · 4,2 (plank) + 0,18 (räcke) = 0,92 kN/m

Trafiklast

• Vertikal trafiklast, ytlast, q_fk = 2,0 + 120 / (L + 30) kN/m², och 2,5 kN/m² ≤ q_fk ≤ 5,0 kN/m²,
  vilket ger q_fk = 4,93 kN/m² om L = 11 m, det vill säga 4,93 kN/m per limträbalk
• Horisontell trafiklast längs bron, Q_flk = 10 % av total vertikal trafiklast,
  det ger Q_flk = 0,10 · 2 · 11 · 4,93 = 10,85 kN, det vill säga 5,42 kN per limträbalk
• Koncentrerad vertikal last: Q_fwk=10 kN på lastyta 0,1 x 0,1 m² för kontroll av lokala effekter.

Vindlast

• Horisontell vindlast i riktning tvärs bron, F_wx = ρ/2·v_b²·C·A_ref,x = 0,303 · 6,3 · 15,2 = 29,0 kN och 29,0/11/2 =
  1,32 kN/m per limträbalk, där
  ρ/2·v_b² = 1,25 / 2 · 22² = 0,303 kN/m² (antag: v_b = 22 m/s och ρ = 1,25 kg/m³),
  C = 6,3 för b/d_tot = 2 / (1,4 + 0,78) = 0,92 och referenshöjd z_e ≤ 20 m,
  A_ref,x = (0,6 m + balkens, syllens, plankens höjd) · L = (0,6 + 0,78) · 11 = 15,2 m². 
• Vertikal vindlast, F_wz = ρ/2·v_b²·c_e·c_f,z·A_ref,z = 0,303 · 2,4 · 0,9 · 22,0 = 14,40 kN, och 14,40/11/2 = 0,65 kN/m per limträbalk, där
  ρ/2·v_b² = 1,25 / 2 · 22² = 0,303 kN/m² (antag: v_b = 22 m/s och ρ = 1,25 kg/m³),
  c_e=2,4 och c_f,z=0,9 för z_e= 10 m och terräng II,
  A_ref,z = planytan = 2 · 11 = 22 m².
• Horisontell vindlast i riktning längs bron, F_wy = 0,25·F_wx = 0,25 · 29,0 = 7,2 kN, eller 3,6 kN/m per limträbalk

Räcke

• Räckets infästning beräknas för en kraft av 1,0 kN/m, som verkar som variabel last horisontellt eller vertikalt på toppföljaren.

Lastkombinationer och dimensionerande lastvärden

Lastkombinationer enligt SS-EN 1990:2004 och SS-EN 1990:A1/2005

Limträbalkar

Lastfall i brottgränstillståndet, säkerhetsklass 2 ger γ_d = 0,91
Vertikal last per balk
Egentyngd = γ_d·0,89·1,35·G_k = 0,91 · 0,89 · 1,35 · 0,92 = 1,01 kN/m
Trafiklast, ytlast = γ_d·1,5·q_fk = 0,91 · 1,5 · 4,93 = 6,73 kN/m
Trafiklast, ytlast = γ_d·1,5·ψ₀·q_fk = 0,91 · 1,5 · 0,4 · 4,93 = 2,69 kN/m, kombinationsvärdet för variabel last, för kombination med vindlasten som huvudlast
Vindlast = γ_d·1,5·F_wz = 0,91 · 1,5 · 0,65 = 0,89 kN/m
Vindlast = γ_d·1,5·ψ₀·F_wz = 0,91 · 1,5 · 0,3 · 0,65 = 0,27 kN/m, kombinationsvärdet för variabel last, för kombination med trafiklasten som huvudlast

Horisontell last per balk
Vindlast tvärs bron= γ_d·1,5·F_wx = 0,91 · 1,5 · 1,32 = 1,80 kN/m
Vindlast tvärs bron= γ_d·1,5·ψ₀·F_wx = 0,91 · 1,5 · 0,3 · 1,32 = 0,54 kN/m, kombinationsvärdet för variabel last, för kombination med trafiklasten som huvudlast
Vindlast längs bron = γ_d·1,5·F_wy = 0,91 · 1,5 · 3,6 = 4,91 kN
Vindlast längs bron = γ_d·1,5·ψ₀·F_wy = 0,91 · 1,5 · 0,3 · 3,6 = 1,47 kN, kombinationsvärdet för variabel last, för kombination med trafiklasten som huvudlast
Trafiklast längs bron = γ_d·1,5·Q_flk = 0,91 · 1,5 · 5,42 = 7,40 kN
Trafiklast längs bron = γ_d·1,5·ψ₀·Q_flk = 0,91 · 1,5 · 0,4 · 5,42 = 2,96 kN, kombinationsvärdet för variabel last, för kombination med vindlasten som huvudlast

Lastfall i bruksgränstillståndet

Vertikal last per balk
Egentyngd = 1,0·G_k = 1,0·0,92 = 0,92 kN/m
Trafiklast, ytlast = 1,0·q_fk = 1,0 · 4,93 = 4,93 kN/m, för karakteristisk lastkombination
Trafiklast, ytlast =1,0·ψ₁·q_fk = 1,0 · 0,4 · 4,93 = 1,98 kN/m, med faktor för frekvent lastkombination

Syllar

Lastfall i brottgränstillståndet, säkerhetsklass 2 ger γ_d = 0,91

Vertikal last per syll
Egentyngd = γ_d·0,89·1,35·G_k = 0,91 · 0,89 · 1,35 · (0,07 · 0,120 · 4,2 + 0,07 · 0,6 · 4,2) = 0,23 kN/m
Trafiklast, ytlast = γ_d·1,5·q_fk·s = 0,91 · 1,5 · 4,93 · 0,6 = 4,04 kN/m

Lastfall i bruksgränstillstånd

Egentyngd = 1,0·G_k = 1,0·(0,035 + 0,176) = 0,21 kN/m
Trafiklast, ytlast = 1,0·q_fk·s = 1,0 · 4,93 · 0,6 = 2,96 kN/m, för karakteristisk lastkombination
Trafiklast, ytlast = 1,0·ψ₁·q_fk·s = 1,0 · 0,4 · 4,93 · 0,6 = 1,18 kN/m, med faktor för frekvent lastkombination

Slitplank

Lastfall i brottgränstillståndet, säkerhetsklass 2 ger γ_d = 0,91

Egentyngd = γ_d·0,89·1,35·G_k = 0,91 · 0,89 · 1,35 · (0,07 · 0,195 · 4,2) = 0,06 kN/m
Trafiklast, ytlast = γ_d·1,5·q_fk·s = 0,91 · 1,5 · 4,93 · 0,195 = 1,31 kN/m
Koncentrerad last = γ_d·1,5·Q_fwk = 0,91 · 1,5 · 10 = 13,65 kN

Lastfall i bruksgränstillstånd

Egentyngd = 1,0·G_k = 1,0 · 0,057 = 0,057 kN/m
Trafiklast, ytlast = 1,0·q_fk·s = 1,0 · 4,93 · 0,195 = 0,96 kN/m, för karakteristisk lastkombination
Trafiklast, ytlast = 1,0·ψ₁·q_fk·s = 1,0 · 0,4 · 4,93 · 0,195 = 0,39 kN/m, med faktor för frekvent lastkombination

Räcke

Lastfall i brottgränstillstånd, säkerhetsklass 2 ger γ_d = 0,91

Horisontell last per räckesstolpe blir
Räckeslast = γ_d·1,5·q_k ∙ centrumavstånd = 0,91 ∙ 1,5 ∙ 1,0 ∙ 1,8 = 2,5 kN

Materialvärden

Dimensionerande materialvärden enligt SS-EN 1995-1-1:2004. Balkbron hänförs till klimatklass 3.
Dimensionerande värden för hållfasthet i brottgränstillstånd

\(f_d = \frac{k_{mod} \cdot f_k}{\gamma_M}\)

där k_mod = 0,70 för limträ och trä i klimatklass 3 och med korttidslast (trafiklast).
Storleksfaktor vid böjning och drag för limträ (vid h < 600 m) är

\(k_h = min \begin{cases} \left(\frac{600}{h}\right)^{0,1} \\ 1,1 \end{cases}\)

och storleksfaktor för trä (vid h < 150 m) är

\(k_h = min \begin{cases} \left(\frac{150}{h}\right)^{0,2} \\ 1,3 \end{cases}\)

där h är höjd vid böjning eller bredd vid drag.
 
För limträ med höjden 585 mm blir k_h = 1,0.
För trä med höjden 120 mm blir k_h = 1,04 och med höjden 70 mm blir k_h = 1,16.

Limträ i hållfasthetsklass CE L40c

γ_M = 1,25
Böjning: f_m,k = 30,8 N/mm² och f_m,d = 1,0 · 0,70 · 30,8 / 1,25 = 17,2 N/mm²
Tryck parallellt fibrerna: f_c,0,k = 25,4 N/mm² och f_c,0,d = 0,70 · 25,4 / 1,25 = 14,2 N/mm²
Elasticitetsmodul: E_0,mean = 13000 N/mm² och E_0,05 = 10500 N/mm²

Tryckt konstruktionsdel med risk för knäckning:

Knäckfaktor  \(k_{c,y} = \frac{1}{k_y + \sqrt{{k_y}^2 - {\lambda_{rel,y}}^2}}\)

där  \(\lambda_{rel,y} = \frac{\lambda_y}{\pi}\sqrt{\frac{f_{c,0,k}}{E_{0,05}}}\)

och  \(k_y = 0,5 \cdot \left(1 + \beta_c \cdot(\lambda_{rel,y} - 0,3)+
{\lambda_{rel,y}}^2 \right)\)

där \(\beta_c=0,1\) för limträ.

Med \(h=0,585\) m och \( L_c = 11\) m erhålls  \(\lambda_y = \frac{L_c}{i}= \frac{11\cdot
\sqrt{12}}{0,585}=65\)

Vilket ger \(\lambda_{rel,y} = 1,02 > 0,3 \) och risk för knäckning ska beaktas enligt SS-EN 1995-1-1

\( k_y = 1,05 \) ger knäckfaktor \(k_{c,y}=0,77\)

Konstruktionsvirke i hållfasthetsklass C24

γ_M = 1,3
Böjning: f_m,k = 24 N/mm² och f_m,d = 1,04 · 0,7 · 24 / 1,3 = 13,4 N/mm² för höjden 120 mm, f_m,d = 1,16 · 0,7 · 24 / 1,3 = 15,0 N/mm² för höjden 70 mm
Tryck parallellt fibrerna: f_c,0,k = 21 N/mm² och f_c,0,d = 0,7 ·21 / 1,3 = 11,3 N/mm²
Elasticitetsmodul: E_0,mean = 11000 N/mm² och E_0,05 = 7400 N/mm²

Tryckt konstruktionsdel med risk för knäckning (räcke):
β_c = 0,2 för trä. Med h = 0,070 m och L_c = 0,95 m erhålls λ_y = 47
vilket ger λ_rel,y = 0,80 > 0,3 och risk för knäckning
k_y = 0,87 ger knäckfaktor k_c,y = 0,83

2. Dimensionering i brottgränstillstånd

Limträbalkar

Enligt Trafikverkets TRVK Bro ska träbro med spännvidd större än 8 m ha tvärförband mellan huvudbalkar vid upplag. Om man sätter in ytterligare tvärförband till exempel vid tredjedelspunkterna, så samverkar balkarna vid vindlast tvärs bron. Dessutom får man en lastfördelning via brobanan, men den tas oftast inte med vid dimensionering. Samverkan mellan balkarna antas förhindra risk för vippning. Limträbalkarna dimensioneras som fritt upplagda balkar.

Vertikal trafiklast som huvudlast

Dimensionerande böjmoment av vertikal last av egentyngd, trafiklast och vindlast för en balk upplagd på två stöd blir

\(M_{z,d} = \frac{q \cdot l^2}{8} = \frac{(1,01 + 6,73 + 0,27)\cdot 11^2}{8}
= 121,1 \:\text{kNm}\) kNm

Dimensionerande böjspänning blir

\(\sigma_{m,z,d} = \frac{M_{z,d}}{W_z} = \frac{121,1 \cdot 10^6 \cdot 6}{165 \cdot 585^2}=12,87\) N/mm² < f_m,z,d = 17,2 N/mm²

Dimensionerande böjmoment av horisontell vindlast tvärs bron för en balk upplagd på två stöd blir

\(M_{y,d} = \frac{q\cdot l^2}{8}=\frac{0,54 \cdot 11^2}{8} = 8,17\) kNm

Dimensionerande böjspänning blir

\( \sigma_{m,y,d} = \frac{M_{y,d}}{W_y} = \frac{8,17 \cdot 10^6 \cdot 6}{585 \cdot 165^2}=3,08 \) N/mm² < f_m,y,d = 17,2 N/mm²

Dimensionerande tryckkraft längs bron blir

\(F_{c,0,d} = 1,47 + 7,40 = 8,87 \:\text{kN}\)

Dimensionerande tryckspänning blir

\(\sigma_{c,0,d} = \frac{F_{c,0,d}}{A} = \frac{8,87 \cdot 10^3}{165 \cdot 585}=0,09\) N/mm2 < k_c,y·f_c,0,d = 0,77 · 14,2 = 10,9 N/mm²

Kontroll vid böjning i två riktningar samt tryckkraft:

\(\frac{\sigma_{c,0,d}}{k_{c,y} \cdot f_{c,0,d}} + \frac{\sigma_{m,z,d}}
{f_{m,z,d}} + k_m \cdot \frac{\sigma_{m,y,d}}{f_{m,y,d}} = \frac{0,09}
{10,9} + \frac{12,87}{17,2} + 0,7 \cdot \frac{3,08}{17,2} = 0,88 < 1\)

Horisontell vindlast tvärs bron som huvudlast

Dimensionerande böjmoment av horisontell vindlast tvärs bron för en balk upplagd på två stöd blir

\(M_{y,d}=\frac{q \cdot l^2}{8} = \frac{1,80 \cdot 11^2}{8}=27,2 \:\text{kNm}\)

Dimensionerande böjspänning blir

\(\sigma_{m,y,d} = \frac{M_{y,d}}{W_y} = \frac{27,2 \cdot 10^6 \cdot 6}{585 \cdot 165^2}=10,25\) N/mm² < f_m,y,d = 17,2 N/mm²

Dimensionerande böjmoment av vertikal last av egentyngd, trafiklast och vindlast tvärs bron för en balk upplagd på två stöd blir

\(M_{z,d}=\frac{q \cdot l^2}{8} = \frac{(1,01 + 2,69 + 0,89) \cdot 11^2}{8}=69,4 \:\text{kNm}
\)

Dimensionerande böjspänning blir

\(\sigma_{m,z,d} = \frac{M_{z,d}}{W_z} = \frac{69,4 \cdot 10^6 \cdot 6}{165 \cdot 585^2}=7,37\) N/mm² < f_m,z,d = 17,2 N/mm²

Dimensionerande tryckkraft längs bron blir

\(F_{c,0,d} = 2,96 + 4,91 = 7,87 \:\text{kN}\)

Dimensionerande tryckspänning blir

\(\sigma_{c,0,d} = \frac{F_{c,0,d}}{A} = \frac{7,87 \cdot 10^3}{165 \cdot 585}=0,08\) N/mm² < k_c,y·f_c,0,d = 0,77 · 14,2 = 10,9 N/mm²

Kontroll vid böjning i två riktningar samt tryckkraft:

\(\frac{\sigma_{c,0,d}}{k_{c,y} \cdot f_{c,0,d}} + \frac{\sigma_{m,z,d}}
{f_{m,z,d}} + k_m \cdot \frac{\sigma_{m,y,d}}{f_{m,y,d}} = \frac{0,08}
{10,9} + \frac{7,37}{17,2} + 0,7 \cdot \frac{10,25}{17,2} = 0,85 < 1\)

\(\frac{\sigma_{c,0,d}}{k_{c,y} \cdot f_{c,0,d}} + k_m \cdot
\frac{\sigma_{m,z,d}}{f_{m,z,d}} + \frac{\sigma_{m,y,d}}{f_{m,y,d}} =
\frac{0,08}{10,9} + 0,7 \cdot \frac{7,37}{17,2} + \frac{10,25}{17,2} =
0,90 < 1\)

Två limträbalkar 165x585 mm klarar alltså vindlastfallet. Om balkarna inte klarar det, kan man öka dimensionen på limträbalkarna eller sätta in ett horisontellt fackverk för vindlasten. Vanligen används fackverk även om inte dimensioneringen kräver det, eftersom det ger en stadigare bro även vid hanteringen.

Syllar

Syllarna dimensioneras som fritt upplagda balkar.

Egentyngd och trafiklast som huvudlast

Dimensionerande böjmoment för en balk upplagd på två stöd:

\(M_{z,d}=\frac{q \cdot l^2}{8} = \frac{(0,23 + 4,04) \cdot 1,835^2}{8}
=1,80 \:\) kNm

Dimensionerande böjspänning blir

\( \sigma_{m,z,d} = \frac{M_{z,d}}{W_z} = \frac{1,80 \cdot 10^6 \cdot 6}
{70 \cdot 120^2}=10,7 \) N/mm² < f_m,z,d = 13,4 N/mm²

Slitplank

Plankorna beräknas som fritt upplagda balkar. Plankorna kan också räknas som kontinuerliga om hänsyn tas till syllarnas eftergivlighet. Plankorna utgör samtidigt beläggning. De bör klara en nedslitning med cirka 5-10 mm innan de måste bytas ut.

Egentyngd och trafiklast som huvudlast

Dimensionerande böjmoment för en balk upplagd på två stöd:

\( M_{z,d}=\frac{q \cdot l^2}{8} = \frac{(0,06 + 1,31) \cdot 0,6^2}{8}
=0,062 \:\) kNm

Dimensionerande böjspänning blir

\(\sigma_{m,z,d} = \frac{M_{z,d}}{W_z} = \frac{0,062 \cdot 10^6 \cdot 6}
{195 \cdot 70^2}=0,39\) N/mm² < f_m,z,d = 15,0 N/mm²

Egentyngd och punktlast

Dimensionerande böjmoment för egentyngd och koncentrerad last (punktlast) för en balk upplagd på två stöd:

\(M_{z,d}=\frac{q \cdot l^2}{8} + \frac{P \cdot l}{4} = \frac{0,06 \cdot
0,6^2}{8} + \frac{13,65 \cdot 0,6}{4} \:\) = 2,05 kNm

Dimensionerande böjspänning blir

\(\sigma_{m,z,d} = \frac{M_{z,d}}{W_z} = \frac{2,05 \cdot 10^6 \cdot 6}
{195 \cdot 70^2}=12,9\) N/mm² < f_m,z,d = 15,0 N/mm²

Räcke

Dimensionerande böjmoment av räckeslast för en konsol:
M_z,d = P ∙ l = 2,5 ∙ 0,7 = 1,75 kNm

Dimensionerande böjspänning blir

\(\sigma_{m,z,d} = \frac{M_{z,d}}{W_z} = \frac{1,75 \cdot 10^6 \cdot 6}
{70 \cdot 120^2}=10,4\) N/mm² < f_m,z,d = 13,4 N/mm²

Snedsträva går ned till syllens ände, cirka 0,5 m utanför räcket, den lutar cirka 50 grader.
Dimensionerande tryckkraft i snedsträva av räckeslasten blir
F_c,d = 4,2 kN
Dimensionerande tryckspänning blir

\(\sigma_{c,0,d} = \frac{F_{c,0,d}}{A} = \frac{4,2 \cdot 10^3}{70 \cdot 120}=0,50\) N/mm² < k_c,y·f_c,0,d = 9,38 N/mm²

Räckesstolpe och snedsträva placeras mellan dubbla syllar och fästs med till exempel genomgående skruv.

3. Dimensionering i bruksgränstillstånd

Limträbalkar

Nedböjning av trafiklast
Enligt TRVK Bro ska dimensionering med avseende på deformationer utföras för frekventa lastkombinationer och beräknad nedböjning i längs- och tvärled av trafiklast inte överstiga 1/400 av den teoretiska spännvidden.

Nedböjning för en balk upplagd på två stöd blir

\(u_{inst} = \frac{5 \cdot q \cdot l^4}{384 \cdot E \cdot I} = \frac{5 \cdot
(0,92 + 1,98) \cdot 10^3 \cdot 11^4 \cdot 12}{384 \cdot 13000 \cdot 10^6 \cdot
0,165 \cdot 0,585^3} = 0,0154 \:\text{m}\)

Nedböjningen överstiger inte L/400 = 11/400 = 0,0275 m.

Svängningar
Enligt SS-EN 1990 bör komfortkriterier för gångtrafikanter (största accepterade acceleration) verifieras om överbyggnadens egenfrekvens är mindre än 5 Hz för vertikala svängningar. Enligt SS-EN 1995-1-1 bör medelvärdet av styvhetsegenskaper användas i bruksgränstillstånd med hänsyn till vibrationer.
Egenfrekvensen för en fritt upplagd balk på två stöd blir

\(f_1=\frac{\pi}{2 \cdot L^2} \cdot \sqrt{\frac{E \cdot I}{m}} =
\frac{\pi}{2 \cdot 11^2} \cdot \sqrt{\frac{13000 \cdot 10^6 \cdot
0,165 \cdot 0,585^3}{\frac{0,92 \cdot 10^3}{9,81}}} = 8,02 \:
\text{Hz}>5\:\text{Hz}\)

där
L = längd, m
E·I = böjstyvhet för tvärsnittet, Nm²
m = massa per längdenhet, kg/m
Eftersom egenfrekvensen är större än 5 Hz behöver ingen ytterligare kontroll göras.

Syllar

Nedböjning
Nedböjning för en balk upplagd på två stöd blir

\(u_{inst} = \frac{5 \cdot q \cdot l^4}{384 \cdot E \cdot I} = \frac{5
\cdot 1,18 \cdot 10^3 \cdot 1,835^4 \cdot 12}{384 \cdot 11000 \cdot 10^6
\cdot 0,070 \cdot 0,120^3} = 0,00157 \:\text{m}\)

Nedböjningen överstiger inte L/400 = 1,835/400 = 0,00459 m.

4. Sammanställning

Balkar: 2 st 165x585 mm, CE L40c
Syllar: 70x120 mm, C24, centrumavstånd 600 mm
Slitplank: 70x195 mm, C24
Tvärförband: 90x450 mm, CE L40c
Räckesstolpar: 70x120 mm, C24, centrumavstånd 1800 mm