Skivverkan för bjälklag

Skjuvpåkänningar

I ett bjälklag i massivträ verkar flera sammanfogade bjälklagsplattor tillsammans som en stor skiva som kan fördela ut horisontella laster till stabiliserande väggar. För att uppfylla krav på bärförmåga i brottgränstillstånd och bruksgränstillstånd krävs att bjälklagselement i massivträ och fogar är tillräckligt hållfasta och styva. Nedan presenteras formler och data som har betydelse för beräkning av spänningar och deformationer inom ett bjälklagselement. Data för olika fogtyper framgår av Tabell 1.

Horisontell last som verkar i bjälklagets plan längs kantsidorna ger skjuvspänningar och skjuvdeformationer medan last som verkar vinkelrätt mot kantsidorna ger böjspänningar och böjdeformationer. I ett stort bjälklag uppbyggt av flera element uppträder den största skjuvpåkänningen vid de stabiliserande väggarna.

 

Brottgränstillstånd	Bruksgränstillstånd
Rk (kN/skruvpar)	kk (kN/mm och skruvpar)
1,51	0,52

¹ Maxlast vid deformationen 9 mm.
² Styvhetsvärdet gäller för deformationer upp till 2 mm.

Tabell 1. Karakteristiska värden för dimensionering av bärförmåga i fogens längdriktning (horisontella skjuvkrafter) för ett limmat plattbjälklag.

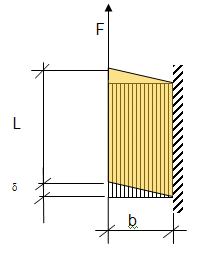
Från de horisontella skjuvkrafter F som verkar på ett bjälklagselement kan skjuvspänningar och skjuvdeformationer beräknas enligt Figur 1.

VY horisontellt	Skjuvspänning (medel)	\(\tau = \frac{F}{L \cdot t}\)	[MPa]
	Skjuvdeformation	\(\delta_{skjuv} = \frac{\tau}{G} \cdot b\)	[m]
	Beteckningar:   F = Kraft [N]   L = Längd bjälklagselement [m]   t = Tjocklek bjälklagselement [m]   b = Bredd bjälklagselement [m]   G = Skjuvmodul [MPa]

Figur 1. Beräkning av skjuvspänning och skjuvdeformation för bjälklag i massivträ.

Böjpåkänningar

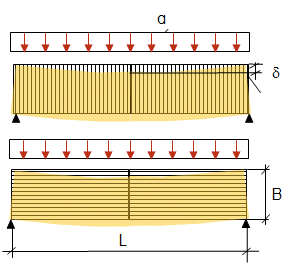
De största böjspänningarna och böjdeformationerna för en lastbärande bjälklagsplatta uppträder vid halva spännvidden. Från de horisontella laster som verkar i bjälklagets plan kan böjspänningar σ och böjdeformationer δ beräknas enligt Figur 2.

VY horisontellt	Dimensionerande böjspänning	\(\sigma_{dim} = \frac{M_{max}}{W} = \frac{\frac{q \cdot L^2}{8}}{\frac{t \cdot B^2}{6}}\)	[MPa]
	Dimensionerande böjdeformation	\(\delta_{dim,böj} = \frac{5 \cdot q \cdot L^4}{384\cdot E \cdot I}\)	[m]
	Beteckningar:   q = Utbredd last [N/m]   Mmax  = Maximalt böjmoment [Nm]   L = Längd bjälklagselement [m]   B = Bredd bjälklagselement [m]   t  = Tjocklek bjälklagselement [m]   W = Motståndsmoment [m3]   EI = Böjstyvhet [Nm2]

Figur 2. Beräkning av böjspänning och böjdeformation för bjälklag i massivträ.

Förskjutning i bjälklagsfog

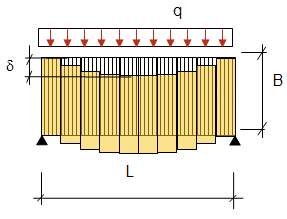
Utifrån den horisontella vindlasten som verkar på bjälklagsskivan beräknas krafter och förskjutningar i fogar. De största skjuvkrafterna och fogförskjutningarna uppträder vid bjälklagets ändupplag. Skjuvkrafter i fogarna och fogförskjutningar mellan flera bjälklagselement kan beräknas enligt Figur 3. Fogförbandets styvhet k_k framgår av Tabell 1.

VY horisontellt	[N]Skjuvkraft i en bjälklagsfog placerad x från ena upplaget \(F_{fog} (x) = q * \left(\frac{L}{2} - x \right) \qquad \left(0 \leq x < \frac{L}{2}\right)\)
	[m]Förskjutning för en bjälklagsfog i fogens längdriktning \(\Delta \delta_i(x_i) = \frac{F_{fog}(x_i)}{k_k}  \qquad \left(0 \leq x < \frac{L}{2}\right)\)
	[m]Summan av delförskjutningarna ger totala förskjutningen \(\delta_{fog} = \Delta\delta_1 + \Delta\delta_2 + \Delta\delta_3 + \dotso \)
	Beteckningar:   Ffog = Kraft i bjälklagsfog [N]   q = Utbredd last [N/m]   x = Lägeskoordinat [m]   L = Längd bjälklagselement [m]   kk = Fogförbandets styvhet [N/m]

Figur 3. Beräkning av förskjutning i bjälklagsfogar för bjälklag i massivträ.

Bjälklagets totala utböjning är summan av bidragen från skjuvning, böjning och förskjutning i bjälklagsfogar.

Bjälklag av flerskikts massivträskivor

I Tabell 2 och 3 anges de materialparametrar som behövs för beräkning av spänningar och deformationer för bjälklag av flerskikts massivträskivor utan fogar. 

	Element som balk
Bjälklag av flerskikts massivträskivor	Skjuvspänning fvk (MPa)	Böjspänning fmkx (MPa)	Böjspänning fmky (MPa)
Tjocklek 95 mm, 5 skikt Tjocklek 125 mm, 5 skikt Tjocklek 145 mm, 5 skikt	2 2 2	5 6 7	7 6 5

Tabell 2. Karakteristiska hållfasthetsvärden för bjälklag av flerskikts massivträskivor för beräkning i brottgränstillstånd.

	Element som balk
Bjälklag av flerskikts massivträskivor	Skjuvmodul Gkxy (MPa)	Elasticitetsmodul Ekx (MPa)	Elasticitetsmodul Eky (MPa)
Tjocklek 95 mm, 5 skikt Tjocklek 125 mm, 5 skikt Tjocklek 145 mm, 5 skikt	500 500 500	5200 6700 5500	7800 7400 7400

Tabell 3. Karakteristiska styvhetsvärden för limmade plattbjälklag för beräkning i bruksgränstillstånd.

Kassettbjälklag

Samma formler som används för plattbjälklag vid beräkning av spänningar och deformationer används även för kassettbjälklag.

Egenskapsvärden för flerskikts massivträskiva med tjocklek 72 mm ingående i kassettbjälklaget, standard, anges i Tabell 4 och 5.

	Element betraktat som balk
Flerskikts massivträskiva	Skjuvspänning fvk (MPa)	Böjspänning fmkx (MPa)	Böjspänning fmky (MPa)
Tjocklek 72 mm, 3 skikt	>2	5	6

Tabell 4. Karakteristiska hållfasthetsvärden för flerskikts massivträskiva till kassettbjälklag för beräkning i brottgränstillstånd.

	Element betraktat som balk
Flerskikts massivträskiva	Skjuvmodul Gkxy (MPa)	Elasticitetsmodul Ekx  (MPa)	Elasticitetsmodul Eky  (MPa)
Tjocklek 72 mm, 3 skikt	500	6700	6700

Tabell 5. Karakteristiska styvhetsvärden för flerskikts massivträskiva till kassettbjälklag för beräkning i bruksgränstillstånd.