Dimensionering av väggar av flerskikts massivträskivor

I de flesta fall sker deformationen i konstruktionens veka riktning och därmed kan reglerna för böjd och tryckt stång tillämpas.

Dimensionering av tryckta massivträkonstruktioner kan göras enligt Boverkets konstruktionsregler, BKR, eller Eurokod 5. För de slanka massivträskivorna är stabilitetsfallet oftast avgörande för väggens bärförmåga.

Även upplagstryck i väggars ändar och mot syll och bjälklag måste kontrolleras.

Dimensionering av väggskivor, vertikal och tranversal last

Dimensionering av väggskivor av massivträ kan göras enligt två alternativ: dimensionering med hjälp av diagram samt dimensionering genom beräkning. 

Dimensionering med hjälp av diagram

a) Bestäm dimensionerande laster i brottgränstillståndet, det vill säga dimensionerande vertikal last F_cd och transversallast Q_d för det aktuella lastfallet. Vanligtvis erfordras ingen dimensionering i bruksgränstillståndet.

b) Bestäm väggens knäcklängd, L_k

c) Bestäm bärförmågan med hjälp av diagram enligt nedan. Diagrammen är beräknade för kortvarigaste lasttyp B, klimatklass 0 och 1, och säkerhetsklass 3 samt att väggen belastas centriskt. För excentriskt belastade väggar görs ett tillägg till den horisontella lasten motsvarande det tillkommande momentet på grund av lastens excentricitet. Bärförmågan jämförs med dimensionerande vertikal last F_cd.

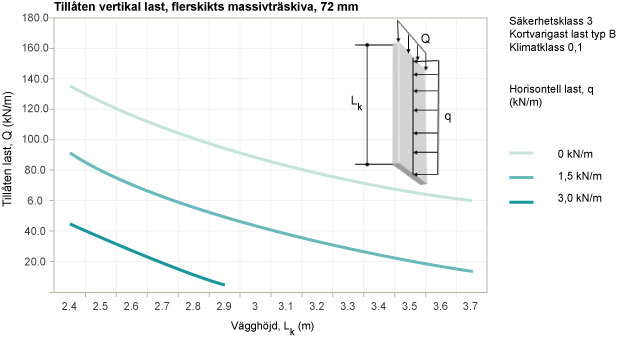
Diagram 1. Tillåten vertikal last för väggar av flerskikts massivträskivor.

Dimensionering genom beräkning, enligt Boverkets konstruktionsregler, BKR

a) Bestäm dimensionerande laster i brottgränstillståndet
Dimensionerande vertikal last F_cd och transversallast Q_d för det aktuella lastfallet. Vanligtvis erfordras ingen dimensionering i bruksgränstillståndet.

b) Beräkna dimensionerande lasteffekter

Dimensionerande normalkraft \(S_{cd} = F_{cd}\)

Dimensionerande moment \(S_{md} = \frac{q_\delta {L_k}^2}{8}\)

c) Beräkna dimensionerande bärförmåga för normalkraft, R_cd
Beräkna dimensionerande tryckhållfasthet, f_cd

d) Beräkna dimensionerande bärförmåga för moment, R_cmd
Beräkna dimensionerande hållfasthet, f_md

Väggens dimensionerande bärförmåga för moment

e) Kontroll av bärförmåga - normalkraft och samtidig böjning
För kontroll av bärförmågan vid samtidigt verkande horisontell och vertikal last tillämpas interaktionsformeln enligt nedan. Vid böjning och tryck där risk för knäckning kan föreligga, det vill säga λ > 27 bör villkoret ≤ 1,0 vara uppfyllt.

\(0,7\Bigl\lvert \frac{S_{md}}{R_{md}} \Bigr\rvert+\Bigl\lvert \frac{S_{cd}}{R_{cd}} \Bigl\lvert \leq 1,0 \)

Tabell 1. Hållfasthet och styvhet för limmade väggelement vid beräkning i brottgränstillstånd.

Dimensionering av väggskivor, last i skivans plan (skivverkan)

Massivträskivor lämpar sig väl för stabilisering av byggnader då de har hög styvhet och bärförmåga. I en byggnad överförs normalt laster från bjälklag till stabiliserande väggar. En hel vägg består av flera väggelement som är sammankopplade med vertikala fogar. Väggelementen utsätts för en horisontell last i väggelementens plan som ger skjuvspänningar och böjspänningar. Spänningarna i materialet ger tillsammans med förskjutningar i fogarna en total deformation i skivans plan på grund av en horisontell last.

\(\delta_{total} = \delta_{skjuv} + \delta_{böj} + \delta_{fog}\)

Från den horisontella kraft som verkar på ett väggelement utan fogar kan skjuvspänning τ (N/mm²) beräknas som

\(\tau = \frac{F}{b \cdot t}\)

skjuvdeformation \(\delta_{skjuv}\) (mm) beräknas som

\(\delta_{skjuv} = \frac{F \cdot h}{b \cdot t \cdot G} \)

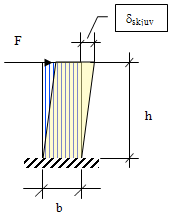
Från den horisontella lasten F som verkar på ett väggelement utan fogar kan
max böjspänning σ (N/mm²) som uppträder vid väggens nedre inspänning beräknas enligt

\(\sigma = \frac{M}{W} = \frac{F \cdot h}{1} \cdot \frac{1}{\frac{t \cdot B^2}{6}}\)

böjdeformationen \(\delta_{böj}\) _böj (mm) beräknas enligt

\(\delta_{böj} = \frac{F \cdot h^3}{3 \cdot E \cdot I}\)

Från den horisontella lasten F som verkar på ett väggparti med vertikala fogar kan de i fogen vertikala krafterna F_v och deformationerna \(\delta_{fog})\ beräknas enligt

\(F_v = F \cdot \frac{h}{b}\)

 \(\delta_{fog} = \gamma \cdot h = \Delta y \cdot \frac{h}{b}\)

 
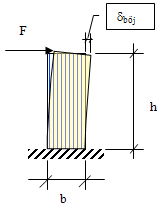
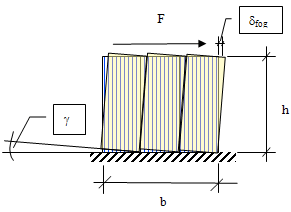
där Δγ är förskjutningen i fogens längdriktning vilken kan beräknas som

\(\Delta y = \frac{F_v}{k_k}\)

 
där k_k är fogförbandets styvhet. 

¹Maxlast vid 9 mm deformation
²Styvhetsvärdet gäller för deformationer upp till 2 mm
 
Tabell 2. Brottgränstillstånd och bruksgränstillstånd för ett förband som består av skruv Spax 5x40 eller likvärdigt och plywoodremsa 12x60 av kvalitet P30. Centrumavståndet mellan skruvar ska vara större än 40 mm.

Tabell 3. Egenskaper hos limmade element för beräkning i bruksgränstillståndet vid belastning i väggelementets plan.