Osymmetriska tvärsnitt, se figur 3.8, kan förekomma även om det bör undvikas då risken ökar för olikartade deformationer och fuktrörelser. Nedan återges en översiktlig metod för att beräkna tvärsnittsstorheter, se ekvationerna 3.28 – 3.31 för osymmetriska tvärsnitt.
Bestämning av tyngdpunkten för tvärsnittet görs enligt följande:
- Ett referensskikt bestäms med Eref som elasticitetsmodul.
- Beräkna tyngdpunkten för varje skikt från tvärsnittets underkant, o1, o2, o3, …oi.
- Beräkna z-koordinaten från tvärsnittets underkant:
-
3.28 \({z_{\rm{s}}} = \frac{{\mathop \sum \nolimits^ \frac{{{E_{\rm{i}}}}}{{{E_{{\rm{ref}}}}}}b \cdot {t_{\rm{i}}}{o_{\rm{i}}}{\rm{\;}}}}{{\mathop \sum \nolimits^ \frac{{{E_{\rm{i}}}}}{{{E_{{\rm{ref}}}}}}b \cdot {t_{\rm{i}}}}}\)
- Nu kan avstånden ai mellan centrum av varje skikt och KL-träskivans neutrallager fastställas:
-
\({\rm a_{\rm{i}}} = \left| {{o_{\rm{i}}} - \;{z_{\rm{s}}}} \right|\)
Beräkning av nettoarea, med bärriktning i x-led:
3.29 \({A_{{\rm{x}},{\rm{net}}}} = \mathop \sum \nolimits^ \frac{{{E_{\rm{i}}}}}{{{E_{{\rm{ref}}}}}}{b_{\mathop{\rm x}\nolimits} }{t_{\rm{i}}}\)
Beräkning av tröghetsmoment, netto, med bärriktning i x-led:
3.30 \({I_{{\rm{x}},{\rm{net}}}} = \mathop \sum \nolimits^ \frac{{{E_{\rm{i}}}}}{{{E_{{\rm{ref}}}}}} \cdot \frac{{{b_\rm x}t_{\rm{i}}^3}}{{12}} + \mathop \sum \nolimits^ \frac{{{E_{\rm{i}}}}}{{{E_{{\rm{ref}}}}}}{b_\rm x}{t_{\rm{i}}}{a_{\rm{i}}}^2\)
Beräkning av böjmotstånd, netto, med bärriktning i x-led:
3.31 \({W_{{\rm{x}},{\rm{net}}}} = \frac{{{I_{{\rm{x}},{\rm{net}}}}}}{{{\rm{max}}\left\{ {\left| {{z_{\rm{ö}}}} \right|;\left| {{z_{\rm{u}}}} \right|} \right\}}}\)
Med zu = zs och zö = h |zs|
Vid bestämning av spänning under böjmoment My,d kan följande användas:
\({\sigma _{{\rm{m}},\rm y,{\rm{d}}}} = \frac{{{E_{\rm{i}}}}}{{{E_{{\rm{ref}}}}}} \cdot \frac{{{M_{{\rm{y}},{\rm{d}}}}}}{{{W_{{\rm{x}},{\rm{net}}}}}}\)
där:
| Ei | är det enskilda skiktets elasticitetsmodul. |
| Eref | är valt referensvärde för elasticitetsmodul. |
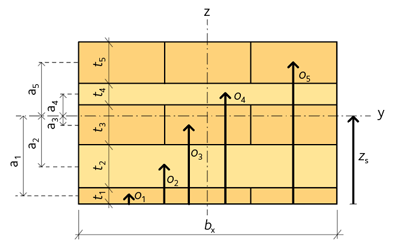
Figur 3.8 Uppbyggnad och numrering av ett osymmetriskt tvärsnitt.

