När KL-träskivor används i en yttervägg kompletteras KL-träskivan allt som oftast med isolering och ett fasadskikt. Fasaden är till för att få ett stationärt klimat i övriga delar av väggen. Vid stationära förhållanden, till exempel vid långa kalla vinterperioder, bestäms värmeflödet genom väggen endast av dess värmegenomgångstal, det så kallade U-värdet. U-värdet är det inverterade värdet av det totala värmemotståndet, R, i en byggnadsdel. En KL-trästomme är i sig isolerande och har få köldbryggor. KL-trä placeras oftast mot den varma sidan och den plana ytan gör att det är enkelt att uppnå bra underlag för kompletterande, ofta heltäckande, isoleringsskikt.
Trä har goda värmeisolerande egenskaper men för att uppfylla de krav vi har idag på klimatskalet krävs ytterligare isolering. En KL-trästomme lämpar sig därvid väl att isolera med någon form av träbaserad isolering, då de båda materialen uppvisar liknande byggfysikaliska egenskaper, även om mineralullsisolering är det vanligaste isolermaterialet i Sverige. Pågående forskning visar på att massiva trästommar kan ha positiv inverkan på en byggnads energiförbrukning.
U-värdet, eller värmegenomgångskoefficienten, talar om hur mycket värme som strömmar genom 1 m2 vägg vid en temperaturskillnad på 1 °C mellan den varma och kalla sidan.
Värmeledningstalet, eller värmekonduktiviteten, för trä beror på träets densitet och fuktkvot. För torr furu och gran med en fuktkvot på cirka 12 % är värmekonduktiviteten, det så kallade lambdavärdet, λ = 0,10 – 0,12 W/m °C, det vill säga cirka tre gånger det värde som gäller för traditionell isolering. Som praktiskt tillämpbart värde brukar man räkna med λ = 0,13 – 0,14 W/m °C.

Isolering av väggelement av KL-trä.
För att beräkna konstruktionens isolerande förmåga kan följande beräkningsgång användas:
a) Bestäm värmekonduktiviteten, λ, för samtliga ingående material, se tabell 9.5. Andra värden kan erhållas ur produktblad, handböcker eller standarder.
b) Bestäm värmemotståndet, R, för luftspalter och värmeövergångsmotstånden, Rsi och Rse. Man skiljer på tre olika typer av luftspalter, se tabell 9.6.
c) Bestäm korrektionsfaktorer, ΔU, för fästanordningar, springor och spalter,
där:
| ΔUf | är en korrektionsterm för extra värmeflöde på grund av mindre fästanordningar i konstruktionen. Termen är oftast försumbar, speciellt för träkonstruktioner. |
| ΔUg | är en korrektionsterm som tar hänsyn till normala utförandefel vid montage av konstruktionen. |
d) Beräkna värmegenomgångskoefficienten för hela konstruktionen.
Om konstruktionen enbart innehåller homogena skikt beräknas varje skikts värmemotstånd och summeras varefter U-värdet kan beräknas enligt ekvationerna 9.3 – 9.5:
9.3 \(R = \frac{d}{\lambda }\quad [\rm {m^2}^\circ C/W]\)
9.4 \({R_{\rm{T}}} = {R_{{\rm{si}}}} + {R_1} + {R_2} + ..{R_{\rm{n}}} + {R_{{\rm{se}}}}\quad [{\rm m^2}^\circ \rm C/W]\)
9.5 \(U = \frac{1}{{{R_{\rm{T}}}}} + \Delta {U_{\rm{g}}} + \Delta {U_{\rm{f}}}\quad [\rm W/{m^2}^\circ C]\)
Vid beräkning av U-värdet för konstruktion som innehåller inhomogena skikt såsom reglar i ett isoleringsskikt ska beräkning av värmegenomgångskoefficienten göras på två sätt enligt SS-EN ISO 6946, U-värdesmetoden och λ-värdesmetoden. Beräkningarna ger ett undre och ett övre värde för det totala värmemotståndet, R. Det värmemotstånd som sedan ska användas för att få fram U-värdet är medelvärdet av de två värmemotstånden.
Vid U-värdesmetoden används vid viktningen areor vinkelrätt mot värmeflödet och vid λ-värdesmetoden viktas ett nytt λ-värde fram för varje inhomogent skikt.
Exempel:
Vägg uppbyggd enligt följande: 13 mm gipsskiva, 100 mm KL-träskiva, ångbroms, 170 mm isoleringsskiva med 12 procent träregelandel, vindskydd, 34 mm luftspalt, 25 mm liggande limträpanel, se figur 9.2.
Vid U-värdesmetoden används vid viktningen areor vinkelrätt mot värmeflödet. I detta fall får vi enbart två areor i det inhomogena skiktet, trä och isolering.
\({A_1} = 0,12 \quad [\rm {m^2}]\)
\({A_2} = 0,88 \quad [\rm {m^2}]\)
Beräkning sker av fyra U-värden, och börjar med att summera ihop motstånden för de två fallen. Värmemotståndet för gipsskivan, KL-träskivan samt de två värmeövergångsmotstånden ingår alltid och summeras till:
\(R = 0,052 + 0,769 + 0,130 + 0,040 = 0,991 \quad [\rm {m^2}^\circ C/W]\)
Fall 1: Area A1, träregel:
\({R_1} = 0,991 + \frac{{0,170}}{{0,14}} = 2,205 \quad [\rm {m^2}^\circ \rm C/W]\)
\({U_1} = \frac{1}{{2,205}} = 0,454 \quad [\rm W/{m^2}^\circ C]\)
Fall 2: Area A2, isoleringsskiva:
\({R_2} = 0,991 + \frac{{0,17}}{{0,037}} = 5,586 \quad [\rm {m^2}^\circ \rm C/W]\)
\({U_2} = \frac{1}{{5,586}} = 0,179 \quad [\rm W/{m^2}^\circ C]\)
U-värden viktas ihop med hjälp av areorna:
\({U_{\mathop{\rm u}\nolimits} } = 0,12 \cdot 0,454 + 0,88 \cdot 0,179 = 0,212 \quad [\rm W/{m^2}^\circ C]\)
vilket ger:
\({R_\rm u} = \frac{1}{{0,212}} = 4,717 \quad [\rm {m^2}^\circ C/W]\)
Vid λ-värdesmetoden viktas ett nytt λ-värde fram för varje inhomogent skikt. Träandelen är 0,12 i det inhomogena skiktet:
\(\lambda = 0,12 \cdot 0,14 + 0,88 \cdot 0,037 = 0,0494 \quad [\rm W/m^\circ C]\)
R-värdet beräknas till:
\({R_{\rm{\lambda}} } = 0,991 + \frac{{0,170}}{{0,0494}} = 4,432 \quad [\rm {m^2}^\circ C/W]\)
Medelvärdet för de två metoderna ger:
\({R_{\mathop{\rm T}\nolimits} } = \frac{{\left( {{R_\rm u} + {R_\lambda }} \right)}}{2} = \frac{{\left( {4,717 + 4,432} \right)}}{2} = 4,575 \quad [\rm {m^2}^\circ C/W]\)
Varefter U-värdet beräknas till:
\(U = \frac{1}{{{R_\rm T}}} + \Delta U = \frac{1}{{4,575}} + 0,01 = 0,23 \quad [\rm W/{m^2}^\circ C]\)
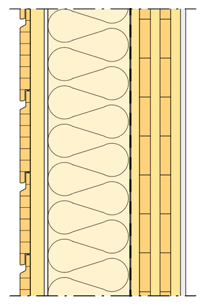
Figur 9.2 Vertikalsnitt genom yttervägg med KL-träskiva.
Tabell 9.5 Värmekonduktivitet för några olika material.
| Material | Värmekonduktivitet, λ (W/m °C) |
| Isolering | 0,04 |
| KL-trä | 0,13 |
| Trä | 0,14 |
| Gipsskiva | 0,24 |
| Betong | 1,7 |
Tabell 9.6 Värmemotstånd för olika luftspalter.
| Luftspalt | Värmemotstånd, R (m2 °C/W) |
| Oventilerade luftspalter | < 0,18 |
| Svagt ventilerade luftspalter | < 0,15 |
| Väl ventilerade luftspalter | 0 |
Tabell 9.7 Värmeövergångsmotstånd för olika byggdelar.
| Byggdel | Värmeövergångsmotstånd, Rsi (m2 °C/W) | Värmeövergångsmotstånd, Rse (m2 °C/W) |
| Väggar | 0,13 | 0,04 |
| Tak | 0,10 | 0,04 |
| Golv | 0,17 | 0,04 |
Tabell 9.8 Exempel på korrektionsterm för ytterväggar.
| Byggdel | ΔU (W/m2 °C) |
| Yttervägg med ett isoleringsskikt med reglar | 0,01 |
| Yttervägg med korslagda reglar | 0 |

