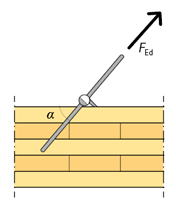
Beräkningar baseras på Eurokod 5. Sambandet mellan last och bärförmåga ska uppfylla kravet enligt ekvation 10.1:
10.1 \(\frac{{{F_{{\rm{Ed}}}}}}{{{F_{{\rm{ax}},{\rm{Rd}}}}}} \le 1\)
Karakteristisk utdragsbärförmåga för en snedställd träskruv med vinkeln α bestäms enligt ekvation 10.2 och ekvation 10.3:
10.2 \({F_{{\rm{ax}},{\rm{k}},{\rm{Rk}}}} = \frac{{{n_{{\rm{ef}}}}{f_{{\rm{ax}},{\rm{k}}}}d{l_{{\rm{ef}}}}{k_{\rm{d}}}}}{{1,2{\rm{co}}{{\rm{s}}^2}\alpha + {\rm{si}}{{\rm{n}}^2}\alpha }}\)
10.3 \({f_{{\rm{ax}},{\rm{k}}}} = 0,52{d^{ - 0,5}}l_{{\rm{ef}}}^{ - 0,1}\rho _\rm k^{0,8}\)
där:
| nef | är effektivt antal träskruvar. |
| fax,k | är karakteristisk utdragshållfasthet vinkelrätt mot fiberriktningen, i N/mm2. |
| d | är yttre gängdiameter i millimeter. |
| \(l\)ef | är träskruvens effektiva förankringslängd i träet för den gängade delen i millimeter. |
| kd | är minimum av d / 8 eller 1. |
| α | är vinkeln mellan träskruvens axel och fiberriktningen, med α ≥ 30°. |
| ρk | är karakteristisk densitet för KL-träet, i kg/m3. |

Moduler av KL-trä.
Dimensionerande utdragsbärförmåga bestäms enligt ekvation 10.4:
10.4 \({F_{{\rm{ax}},{\rm{Rd}}}} = {k_{{\rm{mod}}}}\frac{{{F_{{\rm{ax}},{\rm{k}},{\rm{Rk}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| kmod | är en modifieringsfaktor, här för lastvaraktighetsklass korttid (S). |
| γM | är partialkoefficienten för materialet, här 1,3. |
Dimensionerande last, FEd bestäms utifrån elementets egentyngd samt tillkommande dynamiskt bidrag. Dimensionerande egentyngd Gd kan skrivas enligt ekvation 10.5:
10.5 \({G_{\mathop{\rm d}\nolimits} } = {\gamma _{{\rm{Sd}}}}\left( {{\gamma _{{\mathop{\rm G}\nolimits} ,\rm j}} \cdot G + {\gamma _{{\rm{Q}},1}} \cdot G{\varphi _2}} \right)\)
där:
| γSd | är partialkoefficienten för osäkerhet i beräkningsmodell. |
| γG,j | är partialkoefficienten för permanent last. |
| γQ,1 | är partialkoefficienten för variabel last. |
| φ2 | är en dynamikfaktor. |
10.6 \({\varphi _2} = {\varphi _{2,{\rm{min}}}} + {\beta _2}{v_\rm h}\)
där:
| φ2,min | är en faktor som bestäms av krantyp. |
| β2 | är en faktor som bestäms av krantyp. |
| ν | är lyfthastigheten för kranen. |
Vertikal komposant vid 45° lutning fås enligt:
10.7 \({F_{{\rm{ax}},{\rm{Ed}}}} = \frac{{{G_{\rm{d}}}}}{n}\)
där n är antal lyftpunkter.
Kraftkomposant i lyftriktningen blir då enligt ekvation 10.8:
10.8 \({F_{{\rm{Ed}}}} = \frac{{{F_{{\rm{ax}},{\rm{Ed}}}}\sin {{90}^\circ }}}{{{\rm{sin}}\left( {90 - \beta } \right)}}\)
Kontroll bör även göras av dragbrott i träskruven och kan kontrolleras enligt ekvation 10.9 – 10.11:
10.9 \(\frac{{{F_{{\rm{Ed}}}}}}{{{F_{{\rm{ax}},{\rm{Rd}}}}}} \le 1\)
10.10 \({F_{{\rm{ax}},{\rm{Rd}}}} = {k_{{\rm{mod}}}}\frac{{{F_{{\rm{t}},{\rm{Rk}}}}}}{{{\gamma _{\rm{M}}}}}\)
10.11 \({F_{{\rm{t}},{\rm{Rk}}}} = {n_{{\rm{ef}}}} \cdot {f_{{\rm{tens}},{\rm{k}}}}\)
där:
| ftens,k | är karakteristisk hållfasthet för träskruven vid drag- belastning, uppgift som tillhandahålls av skruvtillverkaren. |
| nef | är effektivt antal träskruvar n enligt nef = n0,9. |