13.4.1 Krav på stagning av pelare

I det idealiserade fallet med helt raka stänger som är fullständigt stagade uppkommer inga stagningskrafter ens vid knäckning eftersom ingen sidoförskjutning förekommer i den stagade punkten. I verkliga konstruktionsdelar uppstår ändå stagningskrafter vid belastning. Som exempel kan tas en serie ledade pelare, var och en utsatt för tryckkraften, P, och stagade med ett stagningssystem. Eftersom pelarna aldrig är absolut lodräta, uppstår en horisontell kraft, F_br, i toppen av varje pelare. Stagningssystemet ska därför ha tillräcklig bärförmåga och styvhet för att motstå resultanten av dessa krafter. Observera att för att vara på den säkra sidan antar man att alla pelare lutar åt samma håll, se figur 13.36.

Ett enkelt antagande är att stagningskraften, F_br, är ungefär 1 – 2 procent av tryckkraften, P. Ett sådant enkelt antagande, utan någon som helst beskrivning på styvhetskravet, är inte nödvändigtvis tillräckligt för att stagningssystemet blir korrekt dimensionerat. Om stagningssystemet är för vekt kan sidoförskjutningen, och därmed stagningskraften, bli oacceptabelt stor. Studera till exempel den elastiska sidostagningen i figur 13.37, där stagningen representeras av en fjäder i pelartoppen med fjäderkonstanten, C.

I det idealiserade fallet med en fullständigt rak pelare kan det påvisas med enkla jämviktsbetraktelser att den så kallade ”ideala fjäderkonstanten”, C_E, alltså den fjäderkonstant som krävs för att uppnå kraften, P_E, som motsvarar Eulers knäckkraft, är:

13.5    \({C_\rm E} = \frac{{{P_\rm E}}}{L}\)

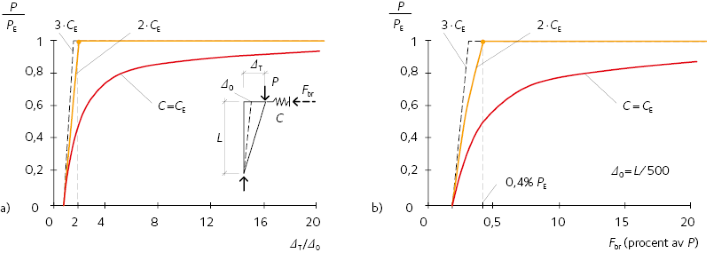
För en pelare som inte är lodrät, visas förhållanden mellan P, C och Δ_T i figur 13.38 a). Om C = C_E, uppnås P_E endast om förskjutningen blir mycket stor. Olyckligtvis ger sådana stora deformationer upphov till stora stagningskrafter F_br, eftersom F_br = C · Δ. Vid praktisk dimensionering ska Δ hållas litet. Detta kan åstadkommas om man väljer C > C_E, till exempel C = 2 · C_E. Om C = 2 · C_E, då är Δ = 2 · Δ₀ när P = P_E, som visas i figur 13.38 a). Det är intressant att observera att ju större fjäderkonstanten är, desto mindre blir stagningskraften, se figur 13.38 b).

Den ovan beskrivna modellen, dock i en något mera komplicerad form, kan också användas för att bestämma den kritiska kraften i en pelare med flera mellanliggande stagningar med samma fjäderkonstant C. Om man antar en typisk initialavvikelse från den räta formen eller förskjutning av toppen för en pelare som är i storleksordningen 1 ⁄ 500 av limträpelarens längd kan ett enkelt dimensioneringsvillkor härledas. På grund av de ovannämnda orsakerna rekommenderas att stagningens fjäderkonstant, C_min, är två gånger den ”ideala” fjäderkonstanten, C_E. I detta villkor ersätts Eulers knäckkraft P_E med det dimensionerande värdet för pelarens tryckkraft P_d, som i praktiken är avsevärt mindre än knäckkraften. Därtill rekommenderas att som värde för stagningskraften, F_br, används åtminstone 1 procent av axialkraften, även om F_br i figur 13.38 b) aldrig överskrider 0,4 procent av axialkraften, om C = 2 · C_E. Orsaken till detta är att initialavvikelsen från den raka formen antas vara Δ₀ = L ⁄ 500. På grund av vindlaster, andra horisontella laster, glapp i skruvförband och annat kan det antagna värdet för Δ₀ överskrida L ⁄ 500. Sålunda kan stagningskraften, F_br, vara större än 0,4 procent av axialkraften.

Bro, Virserum.

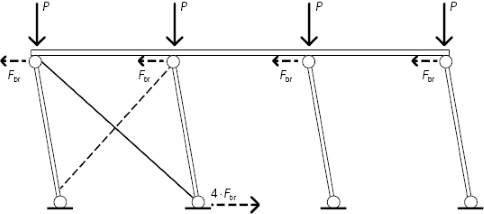
Figur 13.36 Stagningskraften som förorsakas av att pelarna inte är lodräta.

 

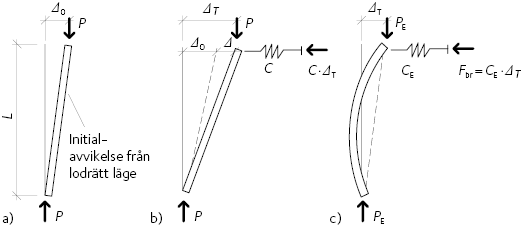
Figur 13.37 Elastisk sidostagning.

 

Figur 13.38 Effekten av initialavvikelse från lodrätt läge.