4.1.1 Böjning och skjuvning

När en massiv rektangulär balk belastas med ett böjmoment M kring den styva (y-y) axeln, är den dimensionerande spänningen vid avstånd z från denna axel enligt linjär elasticitetsteori:

4.1    \(\sigma  = \frac{{M \cdot z}}{{{I_\rm y}}}\)

där I_y är tvärsnittets tröghetsmoment kring y-y axeln. När de största och minsta spänningarna i tvärsnittets övre och undre kant betraktas används elastiska böjmotståndet W_y kring den styva axeln:

4.2    \({W_{\mathop{\rm y}\nolimits} } = \frac{{{I_{\mathop{\rm y}\nolimits} }}}{{\left( {\frac{h}{2}} \right)}} = \frac{{b \cdot {h^2}}}{6}\)

där b är balkens bredd och h balkens höjd. Tvärsnittets största böjspänning fås när balkens dimensionerande böjmoment divideras med böjmotståndet:

4.3    \({\sigma _{\rm m,y,d}} = \frac{{{M_\rm d}}}{{{W_\rm y}}}\)

Motsvarande ekvationer kan härledas för böjning kring den veka balkaxeln (z-z). Om en balk samtidigt utsätts för böjmoment kring båda huvudaxlarna, ska följande dimensioneringsvillkor uppfyllas:

4.4    \(\begin{array}{l} \frac{{{\sigma _{\rm m,y,d}}}}{{{f_{\rm m,y,d}}}} + {k_\rm m}\frac{{{\sigma _{\rm m,z,d}}}}{{{f_{\rm m,z,d}}}} \le 1\\ {k_\rm m}\frac{{{\sigma _{\rm m,y,d}}}}{{{f_{\rm m,y,d}}}} + \frac{{{\sigma _{\rm m,z,d}}}}{{{f_{\rm m,z,d}}}} \le 1 \end{array}\)

där σ_m,y,d och σ_m,z,d är de dimensionerande böjspänningarna kring huvudaxlarna och f_m,y,d och f_m,z,d är de motsvarande dimensioneringsvärdena för böjhållfasthet.

Observera att för limträ är hållfastheten i den veka riktningen inte densamma som den är i den styva riktningen på grund av systemeffekten och lamellernas olika hållfasthetsklasser, se avsnitt 1.3.4. Modifikationsfaktorn k_m beaktar omfördelningen av spänningarna och materialets inhomogenitet. För rektangulära limträtvärsnitt används värdet k_m = 0,7. För övriga tvärsnitt används k_m = 1,0.

Alla balkar utsatta för böjning får också skjuvspänningar parallellt med balkaxeln. Skjuvspänningen är störst vid neutralaxeln och noll vid kanterna. För rektangulära tvärsnitt är den maximala skjuvspänningen τ (vid neutralaxeln):

4.5    \(\tau  = \frac{{3V}}{{2 \cdot b \cdot h}}\)

där V är tvärkraften, b balkens bredd och h balkens höjd. Följande dimensioneringsvillkor ska uppfyllas:

4.6    \({\tau _\rm d} \le {f_{\rm v,d}}\)

där τ_d är den dimensionerande skjuvspänningen och f_v,d är dimensioneringsvärdet för skjuvhållfasthet. Eftersom fuktförändringar kan orsaka sprickbildning i trä, rekommenderar Eurokod 5 att man inte ska använda limträets hela bredd b i ekvation 4.5, utan endast den effektiva bredden b_ef = k_cr ·b, där b_ef < b. Olika värden på k_cr för de olika trämaterialen anges i de nationella bilagorna till Eurokod 5. I Sverige väljs faktorn k_cr utifrån tvärsnittets exponeringsförhållanden och dess värden ges i tabell 4.1.

 

Tabell 4.1 Värden för sprickmodifieringsfaktorn k_cr vid olika exponeringsförhållanden för tvärsnittet.

Exponeringsförhållande	kcr
Inte exponerat för nederbörd och solstrålning	0,86
Helt eller delvis exponerat för nederbörd och solstrålning	0,67

 

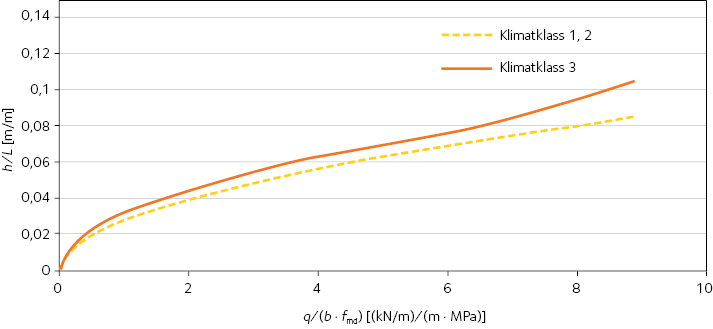 Figur 4.1 Erforderlig balkstorlek uttryckt som förhållandet mellan balkhöjd och spännvidd för olika belastningsnivåer. Beräknat för klimatklass 1, 2 och 3, limträ GL30c. f_md beräknat enligt ekvation 2.9. Dimensioneringsvillkoren är böjspänningar och skjuvspänningar (faktorn k_cr = 0,86 är beaktad). Balkarnas vippning förutsätts vara förhindrad.