Treledsramen är statiskt bestämd och inre krafter i tvärsnittet kan därför beräknas med jämviktsekvationer. Den geometriska formen medför dock ofta ett rätt omfattande beräkningsarbete som med fördel kan utföras med hjälp av dator.
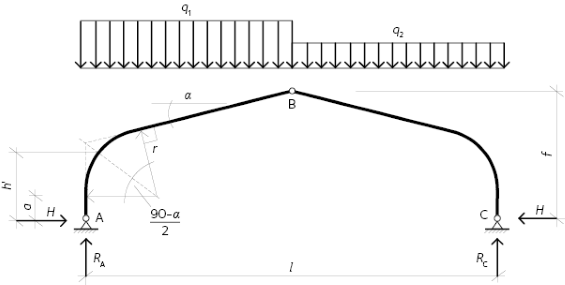
Vid jämnt fördelad, osymmetrisk belastning kan reaktionskrafter och inre krafter för en treledsram enligt figur 10.2 beräknas med hjälp av följande förenklade uttryck.
Observera att ekvation 10.4 och 10.5 gäller för takvinkel α = 14°. För större takvinklar ger dessa ekvationer resultat på säkra sidan.
Vertikal stödreaktion:
10.1 \({R_\rm A} = \frac{{\left( {3 \cdot {q_1} + {q_2}} \right) \cdot l}}{8}\)
10.2 \({R_\rm C} = \frac{{\left( {{q_1} + 3 \cdot {q_2}} \right) \cdot l}}{8}\)
Horisontell stödreaktion:
10.3 \(H = \frac{{\left( {{q_1} + {q_2}} \right) \cdot {l^2}}}{{16 \cdot f}}\)
Maximal normalkraft i ramhörn:
10.4 \(N = 0,79 \cdot \left( {{R_\rm c} - 0,38{q_2}r} \right) + 0,62 \cdot H\)
Maximalt moment i ramhörn:
10.5 \(M = \left( {a + 0,62r} \right) \cdot H - 0,21r \cdot \left( {{R_\rm c} - 0,38{q_2} \cdot r} \right)\)
Tvärkraft i nock (vertikal):
10.6 \({V_\rm B} = \frac{{\left( {{q_1} - {q_2}} \right) \cdot l}}{8}\)
Observera att för treledsramar med ett vertikalt ramben, till exempel en ram med fingerskarvat hörn, kan böjmomentet i ett sådant ramhörn räknas som M = H · h’, se ekvation 10.5 och figur 10.2.